2010年10月10日
秋祭り開催中(lsl+α:任意形状のあたり判定をする)
硬い話になる前に..
Arts Style SIMで開催中の秋祭りです。(10/17日で終了しました)
このブログのネタになっている屋台ははっきり申しまして陰険極まりない代物(※末尾参照)ですが、残りの14台は必見です。

SIM景観をデザインされたRocket BiedermannさんとLieza Noelさんによる屋台はもちろん、ArtsStyle(味噌猫自動車?)のTwinker Tellingさん以下、下野町町内会の皆様が豪華に協賛されています。
場所はこちらです。着地点より順路案内にそって進んでください。
さて。。
出品中のかたぬき屋台の抜き判定に使った線上・外側・内側の判別方法です。
二つ作り、結局設定が楽なので後者を利用しました。

3Dゲームの当たり判定に使われている方法です。SLでは住居のセキュアシステムで立方体範囲の検出に使われている物です(と思います)。
下図の様に、目的の領域を線分で囲んだとき、全ての線分から見て必ず内側にある任意の点Oを一つ用意します。
この時、線分から垂直なベクトルでOが終点であるようなベクトルVOを用意すると、内側か外側か線上か試したい点Pと線分の始点または終点を結んだベクトルVPは以下の関係になります。
1:VPとVOの内積が正⇒点Pは中心側
2:VPとVOの内積がゼロ⇒点Pは線上
3:VPとVOの内積が負⇒点Pは中心と逆側
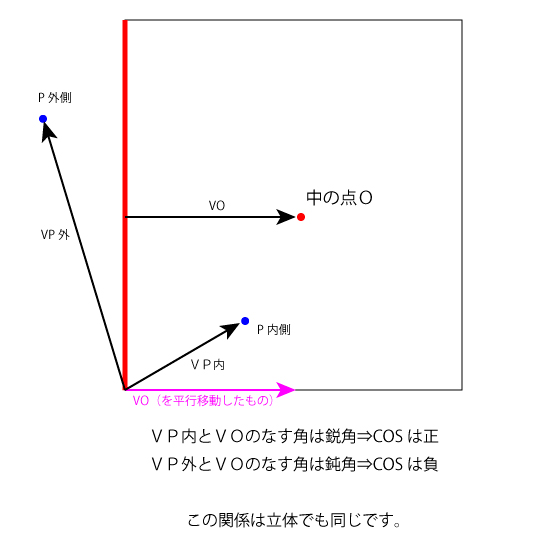
コの字型のように「どの辺から見ても中心であるような点」がない場合には、複数の中の点Oを用意して、図形を分割してやる必要がありますが、上の図の用に中の点Oが共有できるすべての辺とOの内積を取って符号を見て、全部正なら内側、一つでも0なら線上、一つでもマイナスなら外側として、任意の点とのあたり判定を取ることが出来ます。線分に直交するベクトルで中の点Oの方を向いている物を使っても同じ関係になります。
立体で行う場合も関係は同じで、その場合は面に垂直で中の点Oの方を向いているものを採用します。
かたぬきの図形のように曲線で構成されている物の場合は曲線に内接する多角形と外接する多角形を用意して調べることになります。作るだけ作り、設定が面倒ですみやかに挫折しました。(笑
大昔の2Dゲームでドットの重なりで判定していた方法です(と、思います)。
元の画像の内側、外側(ないし線上)など、見分けるべき3者のうち2者を塗りつぶしてしまい、その後ピクセルの色を調べてデーター化し、あらかじめスクリプトに持たせます。
元画像の全ピクセルのデーターを持たせるのが理想ですが圧縮しない限りメモリが足りない為、192*192のエリアに分割して、1,0で表現することにしました。(安直ですがその程度の解像度で十分でしたので。)
表現したい内容が3種類で、値が1、0の二種類しかないですから、外側は0,0,0・・の連続、線上は1、内側は1,0,1,0,1・・・の連続としてビット情報化してあります。
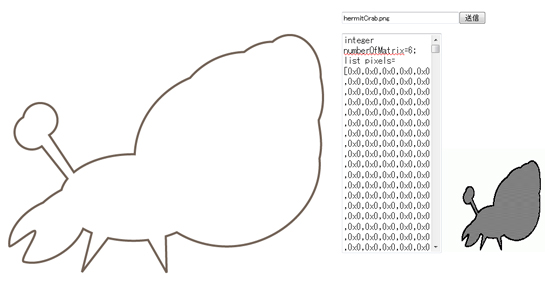
この場合、 llDetectedTouchST()で得られた座標が192*192マスのどれに該当するかを割り出して、次に、その左右(上下方向で走査なら上下)のピクセルの値も取得し、1,0,1または0,1,0であれば内側、そうでない場合自分の座標が1なら線上、そうでないなら外側、で仕分けすることが出来ます。
平面でデーターを作るのは非常に楽ですね。内側と外側を画像処理ライブラリの関数を使って塗りつぶせばおしまいです。立体では六面体ではなく球を使う方が現実的かもしれません。
Arts Style SIMで開催中の秋祭りです。(10/17日で終了しました)
このブログのネタになっている屋台ははっきり申しまして陰険極まりない代物(※末尾参照)ですが、残りの14台は必見です。

SIM景観をデザインされたRocket BiedermannさんとLieza Noelさんによる屋台はもちろん、ArtsStyle(味噌猫自動車?)のTwinker Tellingさん以下、下野町町内会の皆様が豪華に協賛されています。
場所はこちらです。着地点より順路案内にそって進んでください。
さて。。
出品中のかたぬき屋台の抜き判定に使った線上・外側・内側の判別方法です。
二つ作り、結局設定が楽なので後者を利用しました。

1:ベクトルを使う判定方法
3Dゲームの当たり判定に使われている方法です。SLでは住居のセキュアシステムで立方体範囲の検出に使われている物です(と思います)。
下図の様に、目的の領域を線分で囲んだとき、全ての線分から見て必ず内側にある任意の点Oを一つ用意します。
この時、線分から垂直なベクトルでOが終点であるようなベクトルVOを用意すると、内側か外側か線上か試したい点Pと線分の始点または終点を結んだベクトルVPは以下の関係になります。
1:VPとVOの内積が正⇒点Pは中心側
2:VPとVOの内積がゼロ⇒点Pは線上
3:VPとVOの内積が負⇒点Pは中心と逆側

コの字型のように「どの辺から見ても中心であるような点」がない場合には、複数の中の点Oを用意して、図形を分割してやる必要がありますが、上の図の用に中の点Oが共有できるすべての辺とOの内積を取って符号を見て、全部正なら内側、一つでも0なら線上、一つでもマイナスなら外側として、任意の点とのあたり判定を取ることが出来ます。線分に直交するベクトルで中の点Oの方を向いている物を使っても同じ関係になります。
立体で行う場合も関係は同じで、その場合は面に垂直で中の点Oの方を向いているものを採用します。
かたぬきの図形のように曲線で構成されている物の場合は曲線に内接する多角形と外接する多角形を用意して調べることになります。作るだけ作り、設定が面倒ですみやかに挫折しました。(笑
2:塗りつぶしを使う判定方法
大昔の2Dゲームでドットの重なりで判定していた方法です(と、思います)。
元の画像の内側、外側(ないし線上)など、見分けるべき3者のうち2者を塗りつぶしてしまい、その後ピクセルの色を調べてデーター化し、あらかじめスクリプトに持たせます。
元画像の全ピクセルのデーターを持たせるのが理想ですが圧縮しない限りメモリが足りない為、192*192のエリアに分割して、1,0で表現することにしました。(安直ですがその程度の解像度で十分でしたので。)
表現したい内容が3種類で、値が1、0の二種類しかないですから、外側は0,0,0・・の連続、線上は1、内側は1,0,1,0,1・・・の連続としてビット情報化してあります。

この場合、 llDetectedTouchST()で得られた座標が192*192マスのどれに該当するかを割り出して、次に、その左右(上下方向で走査なら上下)のピクセルの値も取得し、1,0,1または0,1,0であれば内側、そうでない場合自分の座標が1なら線上、そうでないなら外側、で仕分けすることが出来ます。
平面でデーターを作るのは非常に楽ですね。内側と外側を画像処理ライブラリの関数を使って塗りつぶせばおしまいです。立体では六面体ではなく球を使う方が現実的かもしれません。
※コツ。以下は必要な方だけ見てください。
斜面に沿って回転させる
lsl 戦車砲をシミュレートする
lsl 連立一次方程式を解く
lsl 多倍長演算
lsl 特定の面のサイズと4隅のリージョン座標を取得する
lsl 座標系の変換(vector)
lsl 戦車砲をシミュレートする
lsl 連立一次方程式を解く
lsl 多倍長演算
lsl 特定の面のサイズと4隅のリージョン座標を取得する
lsl 座標系の変換(vector)
Posted by RBK Drachnyd(しお) at 00:03│Comments(1)
│算数










