2014年03月01日
斜面に沿って回転させる
知人から質問を受けたので久しぶりに。。
下のSSの様に、ある特定の方向(黄色いUFOの方向)を向いているプリムを、


と言う風に斜面に沿って元向いていた方向を維持しながら傾斜させることを考えます。
これは、以前にだらだらと書いておりました、
http://rbk.slmame.com/e971594.html
の変種で、戦車の車体が傾斜している地面、回転させたいプリムが砲塔、そして砲身が無いバージョンになります。
このような場合は、まず、llCastRay()を使って、下の地面の法線ベクトルと、黄色のUFOの方向(つまりllRot2Fwd(llGetRot())を取得します。
法線ベクトルとは、面に垂直な方向を向いている長さ1のvectorの事です。つまり、回転対象の上の面がこのベクトルの方向を向けば良いという事になります。つまり下の図のように回転させればよいという事で、この場合は元々の自分の上方向のベクトルllRot2Up(llGetRot())と、法線ベクトルの間でllRotBetween()を取ってやると回転角の差分が求まります。今の自分の回転にこの回転差分をかけてやると、上面方向は一致します。

上面の傾きが一致しました。ただ、この回転だけを仮に実際にやると、llRot2Up()で上面だけ特定方向を向けたときのように、正面がどこを向くかが不定になります。
そこで、次に、下のSSの様に、その面内で回転して元見ていた黄色のUFOの方向を向けさせます。

この時に少し考え方に工夫を入れてやると、この問題は簡単になります。まず、下の図のように、先に回転させた白線の回転結果と反対に、自分の回転が完全にゼロになるまで、UFOと自分の回転を戻してやります。

具体的には、先に取得しておいた自分の元々の正面方向(UFOの方向)のベクトルを、白線矢印の回転をした後の自分の回転で割ります。
自分の方は、自分の回転を自分の回転で割るので常にZERO_ROTATIONになりますので、<1,0,0>と、<UFOベクトルのX,UFOベクトルのY,0>との間のllRotBetween()を取れば、すぐに平面上での回転方向は定まります。
つまり、手順的には、
1)
自分の正面方向の単位ベクトルllRot2Fwd(llGetRot)を求めておき、
2)
llCastRay()の結果と自分の上方向のノルムllRot2Up(llGetRot)の間の回転角を求め、これを現在の自分の回転にかけた値を先に求め、
3)
1)の正面方向ベクトルを2)の結果の回転で割って回転後のローカル座標系での見かけの方向に直し、次にその結果の上下方向回転だけをゼロにした、つまりZ値だけ0にしたベクトルのノルムを求め、
4)
3)の結果とローカル座標系の正面方向<1,0,0>とのllRotBetweenを取り、
5)
4)の結果に2)の結果をかけたrotationをllSetRot()等する
という手順になります。
この場合は、2)の手順の時にまず一つのベクトルを求め、3)の手順でもう一つのベクトルを求め、これが直交ベクトルになるので4)と2)の合成(5)で3次元回転が一意に決まる、という手順です。また、5)の掛け算の順は、必ず4)に2)をかけなければなりません。これは、4)がローカル回転、2)がグローバル回転になるからです。
他の手順もありますが、3次元回転をベクトルで割り出す場合は基本的に2手順で2つの直交するベクトルを求めて、もう1次元分の向きが自動的に定まるように計算します。
下のSSの様に、ある特定の方向(黄色いUFOの方向)を向いているプリムを、


と言う風に斜面に沿って元向いていた方向を維持しながら傾斜させることを考えます。
これは、以前にだらだらと書いておりました、
http://rbk.slmame.com/e971594.html
の変種で、戦車の車体が傾斜している地面、回転させたいプリムが砲塔、そして砲身が無いバージョンになります。
このような場合は、まず、llCastRay()を使って、下の地面の法線ベクトルと、黄色のUFOの方向(つまりllRot2Fwd(llGetRot())を取得します。
法線ベクトルとは、面に垂直な方向を向いている長さ1のvectorの事です。つまり、回転対象の上の面がこのベクトルの方向を向けば良いという事になります。つまり下の図のように回転させればよいという事で、この場合は元々の自分の上方向のベクトルllRot2Up(llGetRot())と、法線ベクトルの間でllRotBetween()を取ってやると回転角の差分が求まります。今の自分の回転にこの回転差分をかけてやると、上面方向は一致します。

上面の傾きが一致しました。ただ、この回転だけを仮に実際にやると、llRot2Up()で上面だけ特定方向を向けたときのように、正面がどこを向くかが不定になります。
そこで、次に、下のSSの様に、その面内で回転して元見ていた黄色のUFOの方向を向けさせます。

この時に少し考え方に工夫を入れてやると、この問題は簡単になります。まず、下の図のように、先に回転させた白線の回転結果と反対に、自分の回転が完全にゼロになるまで、UFOと自分の回転を戻してやります。

具体的には、先に取得しておいた自分の元々の正面方向(UFOの方向)のベクトルを、白線矢印の回転をした後の自分の回転で割ります。
自分の方は、自分の回転を自分の回転で割るので常にZERO_ROTATIONになりますので、<1,0,0>と、<UFOベクトルのX,UFOベクトルのY,0>との間のllRotBetween()を取れば、すぐに平面上での回転方向は定まります。
つまり、手順的には、
1)
自分の正面方向の単位ベクトルllRot2Fwd(llGetRot)を求めておき、
2)
llCastRay()の結果と自分の上方向のノルムllRot2Up(llGetRot)の間の回転角を求め、これを現在の自分の回転にかけた値を先に求め、
3)
1)の正面方向ベクトルを2)の結果の回転で割って回転後のローカル座標系での見かけの方向に直し、次にその結果の上下方向回転だけをゼロにした、つまりZ値だけ0にしたベクトルのノルムを求め、
4)
3)の結果とローカル座標系の正面方向<1,0,0>とのllRotBetweenを取り、
5)
4)の結果に2)の結果をかけたrotationをllSetRot()等する
という手順になります。
この場合は、2)の手順の時にまず一つのベクトルを求め、3)の手順でもう一つのベクトルを求め、これが直交ベクトルになるので4)と2)の合成(5)で3次元回転が一意に決まる、という手順です。また、5)の掛け算の順は、必ず4)に2)をかけなければなりません。これは、4)がローカル回転、2)がグローバル回転になるからです。
他の手順もありますが、3次元回転をベクトルで割り出す場合は基本的に2手順で2つの直交するベクトルを求めて、もう1次元分の向きが自動的に定まるように計算します。
2010年10月10日
秋祭り開催中(lsl+α:任意形状のあたり判定をする)
硬い話になる前に..
Arts Style SIMで開催中の秋祭りです。(10/17日で終了しました)
このブログのネタになっている屋台ははっきり申しまして陰険極まりない代物(※末尾参照)ですが、残りの14台は必見です。

SIM景観をデザインされたRocket BiedermannさんとLieza Noelさんによる屋台はもちろん、ArtsStyle(味噌猫自動車?)のTwinker Tellingさん以下、下野町町内会の皆様が豪華に協賛されています。
場所はこちらです。着地点より順路案内にそって進んでください。
さて。。
出品中のかたぬき屋台の抜き判定に使った線上・外側・内側の判別方法です。
二つ作り、結局設定が楽なので後者を利用しました。

3Dゲームの当たり判定に使われている方法です。SLでは住居のセキュアシステムで立方体範囲の検出に使われている物です(と思います)。
下図の様に、目的の領域を線分で囲んだとき、全ての線分から見て必ず内側にある任意の点Oを一つ用意します。
この時、線分から垂直なベクトルでOが終点であるようなベクトルVOを用意すると、内側か外側か線上か試したい点Pと線分の始点または終点を結んだベクトルVPは以下の関係になります。
1:VPとVOの内積が正⇒点Pは中心側
2:VPとVOの内積がゼロ⇒点Pは線上
3:VPとVOの内積が負⇒点Pは中心と逆側
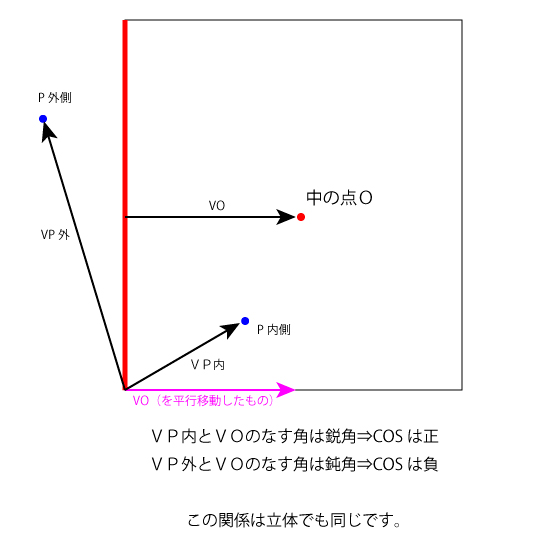
コの字型のように「どの辺から見ても中心であるような点」がない場合には、複数の中の点Oを用意して、図形を分割してやる必要がありますが、上の図の用に中の点Oが共有できるすべての辺とOの内積を取って符号を見て、全部正なら内側、一つでも0なら線上、一つでもマイナスなら外側として、任意の点とのあたり判定を取ることが出来ます。線分に直交するベクトルで中の点Oの方を向いている物を使っても同じ関係になります。
立体で行う場合も関係は同じで、その場合は面に垂直で中の点Oの方を向いているものを採用します。
かたぬきの図形のように曲線で構成されている物の場合は曲線に内接する多角形と外接する多角形を用意して調べることになります。作るだけ作り、設定が面倒ですみやかに挫折しました。(笑
大昔の2Dゲームでドットの重なりで判定していた方法です(と、思います)。
元の画像の内側、外側(ないし線上)など、見分けるべき3者のうち2者を塗りつぶしてしまい、その後ピクセルの色を調べてデーター化し、あらかじめスクリプトに持たせます。
元画像の全ピクセルのデーターを持たせるのが理想ですが圧縮しない限りメモリが足りない為、192*192のエリアに分割して、1,0で表現することにしました。(安直ですがその程度の解像度で十分でしたので。)
表現したい内容が3種類で、値が1、0の二種類しかないですから、外側は0,0,0・・の連続、線上は1、内側は1,0,1,0,1・・・の連続としてビット情報化してあります。
この場合、 llDetectedTouchST()で得られた座標が192*192マスのどれに該当するかを割り出して、次に、その左右(上下方向で走査なら上下)のピクセルの値も取得し、1,0,1または0,1,0であれば内側、そうでない場合自分の座標が1なら線上、そうでないなら外側、で仕分けすることが出来ます。
平面でデーターを作るのは非常に楽ですね。内側と外側を画像処理ライブラリの関数を使って塗りつぶせばおしまいです。立体では六面体ではなく球を使う方が現実的かもしれません。
Arts Style SIMで開催中の秋祭りです。(10/17日で終了しました)
このブログのネタになっている屋台ははっきり申しまして陰険極まりない代物(※末尾参照)ですが、残りの14台は必見です。

SIM景観をデザインされたRocket BiedermannさんとLieza Noelさんによる屋台はもちろん、ArtsStyle(味噌猫自動車?)のTwinker Tellingさん以下、下野町町内会の皆様が豪華に協賛されています。
場所はこちらです。着地点より順路案内にそって進んでください。
さて。。
出品中のかたぬき屋台の抜き判定に使った線上・外側・内側の判別方法です。
二つ作り、結局設定が楽なので後者を利用しました。

1:ベクトルを使う判定方法
3Dゲームの当たり判定に使われている方法です。SLでは住居のセキュアシステムで立方体範囲の検出に使われている物です(と思います)。
下図の様に、目的の領域を線分で囲んだとき、全ての線分から見て必ず内側にある任意の点Oを一つ用意します。
この時、線分から垂直なベクトルでOが終点であるようなベクトルVOを用意すると、内側か外側か線上か試したい点Pと線分の始点または終点を結んだベクトルVPは以下の関係になります。
1:VPとVOの内積が正⇒点Pは中心側
2:VPとVOの内積がゼロ⇒点Pは線上
3:VPとVOの内積が負⇒点Pは中心と逆側

コの字型のように「どの辺から見ても中心であるような点」がない場合には、複数の中の点Oを用意して、図形を分割してやる必要がありますが、上の図の用に中の点Oが共有できるすべての辺とOの内積を取って符号を見て、全部正なら内側、一つでも0なら線上、一つでもマイナスなら外側として、任意の点とのあたり判定を取ることが出来ます。線分に直交するベクトルで中の点Oの方を向いている物を使っても同じ関係になります。
立体で行う場合も関係は同じで、その場合は面に垂直で中の点Oの方を向いているものを採用します。
かたぬきの図形のように曲線で構成されている物の場合は曲線に内接する多角形と外接する多角形を用意して調べることになります。作るだけ作り、設定が面倒ですみやかに挫折しました。(笑
2:塗りつぶしを使う判定方法
大昔の2Dゲームでドットの重なりで判定していた方法です(と、思います)。
元の画像の内側、外側(ないし線上)など、見分けるべき3者のうち2者を塗りつぶしてしまい、その後ピクセルの色を調べてデーター化し、あらかじめスクリプトに持たせます。
元画像の全ピクセルのデーターを持たせるのが理想ですが圧縮しない限りメモリが足りない為、192*192のエリアに分割して、1,0で表現することにしました。(安直ですがその程度の解像度で十分でしたので。)
表現したい内容が3種類で、値が1、0の二種類しかないですから、外側は0,0,0・・の連続、線上は1、内側は1,0,1,0,1・・・の連続としてビット情報化してあります。

この場合、 llDetectedTouchST()で得られた座標が192*192マスのどれに該当するかを割り出して、次に、その左右(上下方向で走査なら上下)のピクセルの値も取得し、1,0,1または0,1,0であれば内側、そうでない場合自分の座標が1なら線上、そうでないなら外側、で仕分けすることが出来ます。
平面でデーターを作るのは非常に楽ですね。内側と外側を画像処理ライブラリの関数を使って塗りつぶせばおしまいです。立体では六面体ではなく球を使う方が現実的かもしれません。
※コツ。以下は必要な方だけ見てください。
2010年09月26日
lsl 戦車砲をシミュレートする
表題の相談を受けまして作成しましたが、内容の説明はチャットだけではつらい為、中身の説明が主な目的となります。
とりあえず、動画から詳しい動きを解析しました。
1.砲塔そのものは車体の現在の傾きに対して何かを中心に左右にだけ回転すること。
2.砲身は砲塔の現在の傾きに対して付け根を中心にして上下にだけ回転すること。
3.限界の回転速度が各々あること。
4.1、2、3を合成した結果が照準に追随すること。
という動き方をしているようです。
車体が回転していない状況では、対空砲と基本的に同じです。ただし、水平回転と垂直回転を各々砲塔、砲身に分担させればよいということになります。
車体の回転や砲塔の回転を考慮する今回の場合は、対空砲ではリージョン座標(SIMの座標)系で水平垂直の回転の合成として向くべき方向をそのまま計算していたものを、対象の方向を自分の土台(ルートまたは砲塔)のローカル座標系に変換してから水平垂直の回転の合成に置き換えることになります。
この種の直交座標系の変換は、自分の回転状態の逆回転で絶対座標系の値(ベクトル)を回転させ、自分は回転していないものと見做してもろもろの計算を行います。位置関係が必要であれば自分の絶対座標系での座標を目標の座標から引きます。

次に、砲塔も砲身も回転中心がプリムの中心(スクリプトで回転させる際の実際の回転中心)とはずれていますので、vectorの回転の方法を使って回転中心をずらして表現します。(下図)
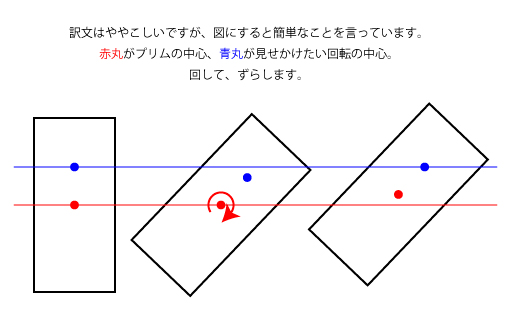
砲身は自身の偏心だけでなく、砲塔の旋回による位置変更も伴います。これらも上図と同様に位置変更を計算して合成する必要があります。
4.は照準を指すまでの回転と移動を特定の距離・回転角度に抑え込んで補間移動するという事になりますので、位置移動と回転について姿勢の補間を使って、さらに最初~最後までの変更速度を一定にするために、何らかの基準になる変更速度との比を用いて表現します。
この種の中間姿勢の補間方法は一般式にすると
その時刻の姿勢=始点の姿勢×Fstart(T)+終わりの姿勢×Fend(T)
(但T=0.0(始点)~1.0(終点)、Fstart(T)+Fend(T)=1.0で一定の関数)
です。
与えるTの値が0~1に変化していくときに、Tの値によって始点と終点の合成された姿勢が戻ってきます。また、Tの刻み幅が一定で変化するときに戻る姿勢の刻み幅は関数Fstart(X)、Fend(X)の戻りに依存します。普通は姿勢の刻みが一定に見えるように関数を作りますので、たとえば180度を回転する場合のTの刻み(⊿T0)をあらかじめ決めておいて、
今回のTの刻み=⊿T0*PI/今回の始点から終点までの回転角度
として用いれば良いでしょう。
移動には線形補間を、回転には球面線形補間を使うのが普通だと思います。
今回の運動では回転ですべてが表現されていますので、rotationの球面線形補間を使うことになります。なお、クオータニオンの補間内部で使う4次元ベクトルの内積のアークコサインは、180度での値はPI_BY_TWOになります。ですので、Tの刻みは、
今回のTの刻み=⊿T0*PI_BY_TWO/今回の始点と終点のrotationの内積の値のアークコサイン
とします。
次に、スクリプトの作りを少し考察します。
リンクされたプリムを回転させる場合、なめらかに動作するllSetLinkPrimitiveParamsFast()を利用することを前提とします。
照準の取得はタイマーなりlink_messageなりになるかと思われますが、rotationの座標系を回転処理本体に合わせることを要求すると、クオータニオンの知識が利用者にも必要となる可能性があるため、利用の便利さを考えますと、照準による戦車砲の回転の始点と終点は、標準の関数で簡単に割り出せ、扱いも簡単なベクトルで設定する事にしておいて、処理側でローテーションに勝手に変換する形で指定させる方が汎用性は高くなると思われます。
ルートが直接回転操作の対象となる様な(つまり砲塔や砲身がルートプリムであるような)乗り物はまずないと思いますので、回転操作の対象は子プリムに限定します。
メンテナンス性は子プリムにスクリを入れるよりルートにすべてを入れた方がよいのではないかと思いますので、プリム番号の取得のような物を使ってあらかじめ対象の番号を設定することを前提にして、ルートから操作することにしました。
全てスクリプトの冒頭に集めておき、ここだけ修正すればよいようにしています。
TARGET_PRIM_NUMBER
スクリプトが回転操作を行う対象のリンク番号を設定します。1以下の数字(ルートを表す)の場合は実行されません。
SYNC_PRIM_NUMBER
FALSEまたは砲塔のリンク番号を設定します。リンク番号が指定の場合はそのプリムの回転によって相対位置を保ちながら補正します。FALSEの場合はルートとの相対位置を維持しようとします。
ENABLED_RL
TRUEにすると左右に旋回します。FALSEにすると左右旋回しません。
ENABLED_UD
TRUEにすると上下に旋回します。FALSEにすると上下旋回しません。
DECENTERING
回転中心の、プリムの中心からのずれをvectorで指定します。
VEC_END
この変数に照準の方向(目標を指差すベクトル)を指定します。初期状態で特定方向を向ける場合などには、ここに方向を示すリージョン座標を設定をしておけばそちらを向きますが、内部で上書きされる変数のため、別途デフォルトの向きを指定する変数を用意しない限り、普通は意味がないと思われます。
DT_PI
180度旋回する場合の補間の刻み(T値の刻み幅)を指定します。
小さいほどゆっくり旋回します。1以上の値にするとすぐさま目標の方向を向きます。ゼロ以下の場合は回転しません。
関数 init_params()
スクリプトの保存時とリセットの時に呼び出されます。対象プリムの初期状態の回転と、ルートまたは連動対象との相対位置関係を取得しています。
対象プリム設定がルートを指している場合FALSE、その他はTRUEを返します。
関数 init()
初期化関数ですが何もせずサンプル(センサーイベント)を起動しています。
実行開始時とrezの時に呼び出されます。
sensorイベント
照準設定のサンプルが入っています。
最も近い距離にいるアバターの方向を、自分から見た方向として変数VEC_ENDに設定しています。
カメラ方向などを指定する場合は回転初期値startVecの設定と同じように、llRot2Fwd(カメラ方向)などとすれば良いかと思われます。
また、回転スクリプトがカメラ操作権限を取ることはないと思いますので、実際に乗り物に利用時はセンサーではなくlink_messageなどの中で設定を行うことになり、timerイベント(回転処理本体)の開始もlink_messageの中になるだろうと思われます。
attachイベント
使っていませんが、改造用に変数isAttachにアタッチされているかどうかを設定しています。
timerイベント
実際の回転処理が入っています。
アタッチメント、REZの両者に対応するために、llGetLinkPrimitiveParams()を多用しています。
これは、従来関数のllGet系はアタッチとREZで動作が異なって少々面倒な場合がある為、いつでもリージョン座標系の値しか返さないllGetLinkPrimitiveParams()を使っているという意味です。ルートに置くことを前提にしているためでもありますが、子プリムに入れる場合は従来関数を使用している部分を数か所、適正に修正するだけでよいはずです。(※取消:ルートのローカル回転は依然、ルートのllGetLocalRot()でなければ取れませんでした。)(※再度取消:llGetLinkPrimitiveParams()でPRIM_ROT_LOCALを指定してルートの回転を取れば子プリムに入っていてもアタッチ・REZを問わず動作させられます。同様に回転の実行時にもPRIM_ROT_LOCALを使う方が簡単になります。)
実行の順序的には、
1.与えられた始点と終点のベクトルを現在の自分のローカル座標系から見たrotationに変換
2.微小回転を球面線形補間(関数 interpolationRot())を用いて計算
3.砲身の場合(SYNC_PRIM_NUMBERに値がある)には回転土台をそれとして位置補正を計算
4.回転を実行
となっています。
以下詳細。。
timer()
{
最初に、回転対象がルートは、パラメーターミスのため実行せず戻ります。
if (TARGET_PRIM_NUMBER<=1)
{
llSetTimerEvent(0.0);
return;
}
ルート回転をllGetLocalRot()で取得します。リージョン回転またはアタッチポイントとの相対回転が取得されます。
avRotは正確にはアタッチメント、REZを問わずrootプリム(アバター※)のリージョン回転になりますが、アバターのアニメは含まれない為、アタッチで使用する場合はアニメーションの方ではアタッチ位置の回転が行われない様にしなければなりません。(※修正:気になって調べてみたところllGetRootRotation()と同じ戻りの模様でした。)
rotation rootRot=llGetLocalRot();
rotation avRot=llList2Rot(llGetLinkPrimitiveParams(LINK_ROOT,[PRIM_ROTATION]),0);
座標系の変換処理
照準のベクトルを自分のルートプリムの現在の回転で割ってローカル回転にしています。
vector norm=llVecNorm(startVec/avRot);
vector norm2=llVecNorm(VEC_END/avRot);
旋回土台の回転を取得
rotation parentRot=avRot;
if (SYNC_PRIM_NUMBER)
{
連動対象がある場合はそちらの回転を採用
parentRot=llList2Rot(llGetLinkPrimitiveParams(SYNC_PRIM_NUMBER,[PRIM_ROTATION]),0);
照準のベクトルも連動対象のローカル座標系の単位ベクトルに再設定します。
自分の土台から見た自分自身の回転だけを計算させる方が(恐らく)改造が楽なため、このようにしてあります。(たとえば砲身の仰角・俯角に限界を設ける場合は、このようにしておけば自分のY軸旋回だけを見て限界判定できますので。。)
norm=llVecNorm(startVec/parentRot);
norm2=llVecNorm(VEC_END/parentRot);
}
ベクトルを水平面垂直面回転に変換しています。
正面軸がX軸でない場合はllEuler2Rot()やllRotBetween()の中の値がある座標軸を変更します。
rotation startRot=llEuler2Rot(<0,(llAcos(norm.z)-PI/2.0)*(float)ENABLED_UD,0>)*llRotBetween(<1,0,0>,<norm.x*(float)ENABLED_RL,norm.y*(float)ENABLED_RL,0>);
rotation endRot=llEuler2Rot(<0,(llAcos(norm2.z)-PI/2.0)*(float)ENABLED_UD,0>)*llRotBetween(<1,0,0>,<norm2.x*(float)ENABLED_RL,norm2.y*(float)ENABLED_RL,0>);
T値の刻みを補正しています。
angleBetweenRot()は球面線形補間内で使われるアークコサインの値を返します。
180度旋回時の値PI_BY_TWOをそれで割ってT刻みの初期値に掛けることで見かけの回転速度を一定にします。
dT=1.0;
float a=angleBetweenRot(startRot,endRot);
if (a!=0.0)
{
dT=PI_BY_TWO/a*DT_PI;
}
else
{
無回転のため、処理を終えて戻ります。
llSetTimerEvent(0.0);
return;
}
今回の回転を球面線形補間で計算しています。
Tの値が1以上(回転終了)の場合にはタイマーを停止します。
T+=dT;
if (T>=1.0) llSetTimerEvent(0.0);
rotation rot=interpolationRot(startRot,endRot,T);
位置補正(連動があれば)を計算します。
初期状態では位置は偏心成分と、ルートから見た相対位置として設定します。
vector pos=DECENTERING;
rotation rot_sync=ZERO_ROTATION;
vector pos_sync=RELATIVE_POS;
if (SYNC_PRIM_NUMBER)
{
連動プリムが設定されている場合は値を上書きします。
対象のローカル回転を取得します。連動プリムのリージョン回転をルートのリージョン回転で割って、ローカル回転成分だけを取得します。
rot_sync=parentRot/avRot;
座標移動をルートからのローカル位置関係として計算します。
リージョン座標系での相対移動距離を計算後に、ルートのリージョン回転と逆回転してローカル座標系に移しています。
pos_sync=(RELATIVE_POS*parentRot+llList2Vector(llGetLinkPrimitiveParams(SYNC_PRIM_NUMBER,[PRIM_POSITION]),0)-llList2Vector(llGetLinkPrimitiveParams(LINK_ROOT,[PRIM_POSITION]),0))/avRot;
}
回転を合成します。
自分のデフォルトの回転、今回の回転、土台の回転を合成します。
rot=defaultMyRot*rot*rot_sync;
移動量を合成します。
pos_syncはルートからの移動量となっています。
自分の偏心成分(pos内)は今回の回転全体をかけて方向を修正します。
pos=pos*rot+pos_sync;
さらに回転全体をルートプリムの回転で割ります。(LSLのバグ?のため必要な決まり事です。)
rot=rot/rootRot;
姿勢変更を実行します。
llSetLinkPrimitiveParamsFast(TARGET_PRIM_NUMBER,[PRIM_POSITION,pos,PRIM_ROTATION,rot]);
}
概要
とりあえず、動画から詳しい動きを解析しました。
1.砲塔そのものは車体の現在の傾きに対して何かを中心に左右にだけ回転すること。
2.砲身は砲塔の現在の傾きに対して付け根を中心にして上下にだけ回転すること。
3.限界の回転速度が各々あること。
4.1、2、3を合成した結果が照準に追随すること。
という動き方をしているようです。
構造
車体が回転していない状況では、対空砲と基本的に同じです。ただし、水平回転と垂直回転を各々砲塔、砲身に分担させればよいということになります。
車体の回転や砲塔の回転を考慮する今回の場合は、対空砲ではリージョン座標(SIMの座標)系で水平垂直の回転の合成として向くべき方向をそのまま計算していたものを、対象の方向を自分の土台(ルートまたは砲塔)のローカル座標系に変換してから水平垂直の回転の合成に置き換えることになります。
この種の直交座標系の変換は、自分の回転状態の逆回転で絶対座標系の値(ベクトル)を回転させ、自分は回転していないものと見做してもろもろの計算を行います。位置関係が必要であれば自分の絶対座標系での座標を目標の座標から引きます。

次に、砲塔も砲身も回転中心がプリムの中心(スクリプトで回転させる際の実際の回転中心)とはずれていますので、vectorの回転の方法を使って回転中心をずらして表現します。(下図)

砲身は自身の偏心だけでなく、砲塔の旋回による位置変更も伴います。これらも上図と同様に位置変更を計算して合成する必要があります。
4.は照準を指すまでの回転と移動を特定の距離・回転角度に抑え込んで補間移動するという事になりますので、位置移動と回転について姿勢の補間を使って、さらに最初~最後までの変更速度を一定にするために、何らかの基準になる変更速度との比を用いて表現します。
この種の中間姿勢の補間方法は一般式にすると
その時刻の姿勢=始点の姿勢×Fstart(T)+終わりの姿勢×Fend(T)
(但T=0.0(始点)~1.0(終点)、Fstart(T)+Fend(T)=1.0で一定の関数)
です。
与えるTの値が0~1に変化していくときに、Tの値によって始点と終点の合成された姿勢が戻ってきます。また、Tの刻み幅が一定で変化するときに戻る姿勢の刻み幅は関数Fstart(X)、Fend(X)の戻りに依存します。普通は姿勢の刻みが一定に見えるように関数を作りますので、たとえば180度を回転する場合のTの刻み(⊿T0)をあらかじめ決めておいて、
今回のTの刻み=⊿T0*PI/今回の始点から終点までの回転角度
として用いれば良いでしょう。
移動には線形補間を、回転には球面線形補間を使うのが普通だと思います。
今回の運動では回転ですべてが表現されていますので、rotationの球面線形補間を使うことになります。なお、クオータニオンの補間内部で使う4次元ベクトルの内積のアークコサインは、180度での値はPI_BY_TWOになります。ですので、Tの刻みは、
今回のTの刻み=⊿T0*PI_BY_TWO/今回の始点と終点のrotationの内積の値のアークコサイン
とします。
次に、スクリプトの作りを少し考察します。
リンクされたプリムを回転させる場合、なめらかに動作するllSetLinkPrimitiveParamsFast()を利用することを前提とします。
照準の取得はタイマーなりlink_messageなりになるかと思われますが、rotationの座標系を回転処理本体に合わせることを要求すると、クオータニオンの知識が利用者にも必要となる可能性があるため、利用の便利さを考えますと、照準による戦車砲の回転の始点と終点は、標準の関数で簡単に割り出せ、扱いも簡単なベクトルで設定する事にしておいて、処理側でローテーションに勝手に変換する形で指定させる方が汎用性は高くなると思われます。
ルートが直接回転操作の対象となる様な(つまり砲塔や砲身がルートプリムであるような)乗り物はまずないと思いますので、回転操作の対象は子プリムに限定します。
メンテナンス性は子プリムにスクリを入れるよりルートにすべてを入れた方がよいのではないかと思いますので、プリム番号の取得のような物を使ってあらかじめ対象の番号を設定することを前提にして、ルートから操作することにしました。
設定項目
全てスクリプトの冒頭に集めておき、ここだけ修正すればよいようにしています。
TARGET_PRIM_NUMBER
スクリプトが回転操作を行う対象のリンク番号を設定します。1以下の数字(ルートを表す)の場合は実行されません。
SYNC_PRIM_NUMBER
FALSEまたは砲塔のリンク番号を設定します。リンク番号が指定の場合はそのプリムの回転によって相対位置を保ちながら補正します。FALSEの場合はルートとの相対位置を維持しようとします。
ENABLED_RL
TRUEにすると左右に旋回します。FALSEにすると左右旋回しません。
ENABLED_UD
TRUEにすると上下に旋回します。FALSEにすると上下旋回しません。
DECENTERING
回転中心の、プリムの中心からのずれをvectorで指定します。
VEC_END
この変数に照準の方向(目標を指差すベクトル)を指定します。初期状態で特定方向を向ける場合などには、ここに方向を示すリージョン座標を設定をしておけばそちらを向きますが、内部で上書きされる変数のため、別途デフォルトの向きを指定する変数を用意しない限り、普通は意味がないと思われます。
DT_PI
180度旋回する場合の補間の刻み(T値の刻み幅)を指定します。
小さいほどゆっくり旋回します。1以上の値にするとすぐさま目標の方向を向きます。ゼロ以下の場合は回転しません。
内容(改造のための要旨)
関数 init_params()
スクリプトの保存時とリセットの時に呼び出されます。対象プリムの初期状態の回転と、ルートまたは連動対象との相対位置関係を取得しています。
対象プリム設定がルートを指している場合FALSE、その他はTRUEを返します。
関数 init()
初期化関数ですが何もせずサンプル(センサーイベント)を起動しています。
実行開始時とrezの時に呼び出されます。
sensorイベント
照準設定のサンプルが入っています。
最も近い距離にいるアバターの方向を、自分から見た方向として変数VEC_ENDに設定しています。
カメラ方向などを指定する場合は回転初期値startVecの設定と同じように、llRot2Fwd(カメラ方向)などとすれば良いかと思われます。
また、回転スクリプトがカメラ操作権限を取ることはないと思いますので、実際に乗り物に利用時はセンサーではなくlink_messageなどの中で設定を行うことになり、timerイベント(回転処理本体)の開始もlink_messageの中になるだろうと思われます。
attachイベント
使っていませんが、改造用に変数isAttachにアタッチされているかどうかを設定しています。
timerイベント
実際の回転処理が入っています。
アタッチメント、REZの両者に対応するために、llGetLinkPrimitiveParams()を多用しています。
これは、従来関数のllGet系はアタッチとREZで動作が異なって少々面倒な場合がある為、いつでもリージョン座標系の値しか返さないllGetLinkPrimitiveParams()を使っているという意味です。ルートに置くことを前提にしているためでもあります
実行の順序的には、
1.与えられた始点と終点のベクトルを現在の自分のローカル座標系から見たrotationに変換
2.微小回転を球面線形補間(関数 interpolationRot())を用いて計算
3.砲身の場合(SYNC_PRIM_NUMBERに値がある)には回転土台をそれとして位置補正を計算
4.回転を実行
となっています。
以下詳細。。
timer()
{
最初に、回転対象がルートは、パラメーターミスのため実行せず戻ります。
if (TARGET_PRIM_NUMBER<=1)
{
llSetTimerEvent(0.0);
return;
}
ルート回転をllGetLocalRot()で取得します。リージョン回転またはアタッチポイントとの相対回転が取得されます。
avRotは
rotation rootRot=llGetLocalRot();
rotation avRot=llList2Rot(llGetLinkPrimitiveParams(LINK_ROOT,[PRIM_ROTATION]),0);
座標系の変換処理
照準のベクトルを自分のルートプリムの現在の回転で割ってローカル回転にしています。
vector norm=llVecNorm(startVec/avRot);
vector norm2=llVecNorm(VEC_END/avRot);
旋回土台の回転を取得
rotation parentRot=avRot;
if (SYNC_PRIM_NUMBER)
{
連動対象がある場合はそちらの回転を採用
parentRot=llList2Rot(llGetLinkPrimitiveParams(SYNC_PRIM_NUMBER,[PRIM_ROTATION]),0);
照準のベクトルも連動対象のローカル座標系の単位ベクトルに再設定します。
自分の土台から見た自分自身の回転だけを計算させる方が(恐らく)改造が楽なため、このようにしてあります。(たとえば砲身の仰角・俯角に限界を設ける場合は、このようにしておけば自分のY軸旋回だけを見て限界判定できますので。。)
norm=llVecNorm(startVec/parentRot);
norm2=llVecNorm(VEC_END/parentRot);
}
ベクトルを水平面垂直面回転に変換しています。
正面軸がX軸でない場合はllEuler2Rot()やllRotBetween()の中の値がある座標軸を変更します。
rotation startRot=llEuler2Rot(<0,(llAcos(norm.z)-PI/2.0)*(float)ENABLED_UD,0>)*llRotBetween(<1,0,0>,<norm.x*(float)ENABLED_RL,norm.y*(float)ENABLED_RL,0>);
rotation endRot=llEuler2Rot(<0,(llAcos(norm2.z)-PI/2.0)*(float)ENABLED_UD,0>)*llRotBetween(<1,0,0>,<norm2.x*(float)ENABLED_RL,norm2.y*(float)ENABLED_RL,0>);
T値の刻みを補正しています。
angleBetweenRot()は球面線形補間内で使われるアークコサインの値を返します。
180度旋回時の値PI_BY_TWOをそれで割ってT刻みの初期値に掛けることで見かけの回転速度を一定にします。
dT=1.0;
float a=angleBetweenRot(startRot,endRot);
if (a!=0.0)
{
dT=PI_BY_TWO/a*DT_PI;
}
else
{
無回転のため、処理を終えて戻ります。
llSetTimerEvent(0.0);
return;
}
今回の回転を球面線形補間で計算しています。
Tの値が1以上(回転終了)の場合にはタイマーを停止します。
T+=dT;
if (T>=1.0) llSetTimerEvent(0.0);
rotation rot=interpolationRot(startRot,endRot,T);
位置補正(連動があれば)を計算します。
初期状態では位置は偏心成分と、ルートから見た相対位置として設定します。
vector pos=DECENTERING;
rotation rot_sync=ZERO_ROTATION;
vector pos_sync=RELATIVE_POS;
if (SYNC_PRIM_NUMBER)
{
連動プリムが設定されている場合は値を上書きします。
対象のローカル回転を取得します。連動プリムのリージョン回転をルートのリージョン回転で割って、ローカル回転成分だけを取得します。
rot_sync=parentRot/avRot;
座標移動をルートからのローカル位置関係として計算します。
リージョン座標系での相対移動距離を計算後に、ルートのリージョン回転と逆回転してローカル座標系に移しています。
pos_sync=(RELATIVE_POS*parentRot+llList2Vector(llGetLinkPrimitiveParams(SYNC_PRIM_NUMBER,[PRIM_POSITION]),0)-llList2Vector(llGetLinkPrimitiveParams(LINK_ROOT,[PRIM_POSITION]),0))/avRot;
}
回転を合成します。
自分のデフォルトの回転、今回の回転、土台の回転を合成します。
rot=defaultMyRot*rot*rot_sync;
移動量を合成します。
pos_syncはルートからの移動量となっています。
自分の偏心成分(pos内)は今回の回転全体をかけて方向を修正します。
pos=pos*rot+pos_sync;
さらに回転全体をルートプリムの回転で割ります。(LSLのバグ?のため必要な決まり事です。)
rot=rot/rootRot;
姿勢変更を実行します。
llSetLinkPrimitiveParamsFast(TARGET_PRIM_NUMBER,[PRIM_POSITION,pos,PRIM_ROTATION,rot]);
}
2010年02月22日
lsl 連立一次方程式を解く
プログラムとしては割とありふれた内容で、n次連立一次方程式の未知数達を左辺に、定数を右辺に移動した後に、左辺の未知数の係数達をn*nの正方行列(飛び石リスト)、右辺をn個のリストとして与えると答えを計算して解のリストを戻します。
後々出てくるかどうか不明ですが、一応λの計算用に前進消去部分は外部関数として独立させてあります。
2・23訂正
早速バグが見つかったので訂正(^^;
後々出てくるかどうか不明ですが、一応λの計算用に前進消去部分は外部関数として独立させてあります。
2・23訂正
早速バグが見つかったので訂正(^^;
// www.lsleditor.org by Alphons van der Heijden (SL: Alphons Jano)
//****************************************************************************
//連立一次方程式を解く
//ガウスの消去法による
//第一引数が未知数の係数行列、第二引数が定数項のベクトル
//****************************************************************************
list gauss(list A,list B)
{
integer lenA=llGetListLength(A);
integer len=llFloor(llSqrt((float)lenA));
//チェック
if (len*len!=lenA || len!=llGetListLength(B))
{
return [];
}
A=truangularMatrix(A+B);
B=llList2List(A,-1*len,-1);
A=llDeleteSubList(A,-1*len,-1);
integer i=len-1;
//一つ目の解
list res=[llList2Float(B,-1)/llList2Float(A,-1)];
integer j=1;
//後進代入処理
while (i--)
{
float tmp=0.0;
list tmpList=llList2List(A,i*len,(i+1)*len-1);
while(j--)
{
tmp=tmp+llList2Float(res,-1*(j+1))*llList2Float(tmpList,len-j-1);
}
res=[(llList2Float(B,i)-tmp)/llList2Float(tmpList,i)]+res;
j=llGetListLength(res);
}
return res;
}
//****************************************************************************
//前進消去により行列を上三角行列にする
//当然、出力の対角線成分が行列の固有値のリストになる。
//引数は方程式の左辺(正方行列)+方程式の右辺ベクトルを追加したものでもよい。
//その場合は右辺ベクトルにも変更が行われる。(ガウスの消去法用)
//****************************************************************************
list truangularMatrix(list A)
{
integer lenA=llGetListLength(A);
integer len=llFloor(llSqrt((float)lenA));
//チェック
list B=[];
if (len*len!=lenA)
{
if (len*len+len!=lenA)
{
//正方行列でも方程式でもなかった
return [];
}
else
{
//方程式らしい
B=llList2List(A,-1*len,-1);
A=llDeleteSubList(A,-1*len,-1);
lenA=len*len;
}
}
integer i=0;
while (i<len)
{
integer j=i+1;
while (j<len)
{
integer p=0;
float f=0.0;
do
{
integer q=(i+p)*(len+1);
if (q>=lenA) return [];
f=llList2Float(A,q);
if (f!=0.0)
{
if (p)
{
A=llListInsertList(llDeleteSubList(A,(i+p)*len,(i+p+1)*len-1),llList2List(A,(i+p)*len,(i+p+1)*len-1),i*len);
B=llListInsertList(llDeleteSubList(B,i+p,i+p),llList2List(B,i+p,i+p),i);
}
jump continue;
}
++p;
} while (TRUE);
@continue;
float tmp=llList2Float(A,j*len+i)/f;
A=llListReplaceList(A,[0.0],j*len+i,j*len+i);
integer k=len-i;
while(--k)
{
A=llListReplaceList(A,[llList2Float(A,j*len+i+k)-tmp*llList2Float(A,i*(len+1)+k)],j*len+i+k,j*len+i+k);
}
if (B!=[])
{
B=llListReplaceList(B,[llList2Float(B,j)-tmp*llList2Float(B,i)],j,j);
}
++j;
}
++i;
}
return A+B;
}
//****************************************************************************
//おしまい
//****************************************************************************
//****************************************************************************
//おまけ。
//行列式の値の計算
//第一引数は正方行列または正方行列の末尾に方程式の右辺(定数項のベクトル)を加えたもの
//第二引数がTRUEの場合関数内で上三角行列に変換する。
//第二引数がFALSEの場合は事前に上三角行列に変換しておくこと。
//****************************************************************************
float determinant(list A, integer f)
{
integer lenA=llGetListLength(A);
integer len=llFloor(llSqrt((float)lenA));
float res=1.0;
//チェック
if (len*len!=lenA)
{
if (len*len+len!=lenA)
{
//正方行列でなかった
return 0.0;
}
else
{
//方程式らしい
A=llDeleteSubList(A,-1*len,-1);
lenA=len*len;
}
}
if (f) A=truangularMatrix(A);
integer i=len;
while (i--)
{
res=res*llList2Float(A,i*(len+1));
}
return res;
}
default
{
touch_start(integer total_number)
{
list test=[0,0,1,8,1,4,2,3,4];
list test2=[4,5,3];
llSay(0, llDumpList2String(gauss(test,test2)," , "));
}
}
2010年02月10日
lsl 多倍長演算
何に使うのか。。。といった風ですが(笑)、多倍長整数実数の演算です。
負数に対応しています(はずです。。。(笑))。
以下アルゴリズムです。
検索から飛んで来られる方がおられるようですが、こちらは32ビット符号付整数と(バグがあるとかないとか言う)単精度浮動小数点数しかないLSLという環境用です。乗算や除算には、メモリーが許せばもっと高速なアルゴリズムがあったと思います。
1:足し算引き算
筆算と同じです。9桁づつ文字列から取り出して計算し、繰上げ切り下げを次の桁で行います。
2:掛け算
筆算と同じです。3桁づつ文字列から取り出して計算し、9桁までの繰上げはその場で、10桁以降は次の桁計算に持ち越します。
3:割り算
筆算と同じです。ただし商を求める際に分母先頭8桁と分子先頭8桁を使って仮の商を算出し、手順を簡略化しています。
整数の割り算(longIntDiv())のみ、listが戻りになり、0番が商、1番が剰余になります。
longDiv()では戻りは商のみとなります。
// www.lsleditor.org by Alphons van der Heijden (SL: Alphons Jano)
//****************************************************************
//多倍長実数計算
//****************************************************************
//整数であるか調べ、符号かFALSEを返す
integer isInt(string s)
{
list l=["0","1","2","3","4","5","6","7","8","9","-"];
integer i=llStringLength(s);
if (!i) return FALSE;
if (s=="0") return FALSE;
if (s=="-0") return FALSE;
if (s=="-") return FALSE;
do
{
--i;
if (llListFindList(l,[llGetSubString(s,i,i)])<0) return FALSE;
} while (i);
if (llSubStringIndex(s,"-")==0) return -1;
return 1;
}
//実数であるか調べ、符号かFALSEを返す
integer isFloat(string s)
{
list l=["0","1","2","3","4","5","6","7","8","9","-","."];
integer i=llStringLength(s);
if (!i) return FALSE;
if (s=="0") return FALSE;
if (s=="-0") return FALSE;
if (s=="-") return FALSE;
do
{
--i;
if (llListFindList(l,[llGetSubString(s,i,i)])<0) return FALSE;
} while (i);
if (llSubStringIndex(s,"-")==0) return -1;
return 1;
}
//文字列先頭の指定文字を削除
string ltrim(string s, string t)
{
if (llGetSubString(s,0,0)!=t) return s;
integer i=0;
integer maxI=llStringLength(s);
if (!maxI) return s;
++maxI;
while(i<maxI)
{
++i;
if (llGetSubString(s,i,i)!=t) jump continue;
}
@continue;
return llGetSubString(s,i,maxI);
}
//文字列末尾の指定文字を削除
string rtrim(string s, string t)
{
if (llGetSubString(s,-1,-1)!=t) return s;
integer i=llStringLength(s);
if (!i) return s;
while(i--)
{
if (llGetSubString(s,i,i)!=t) jump continue;
}
@continue;
return llGetSubString(s,0,i);
}
//整数数値文字列の絶対値について大小比較
integer longIntAbsCmp(string a, string b)
{
a=ltrim(a,"-");
b=ltrim(b,"-");
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return 0;
if (a!="" && b=="") return 1;
if (a=="" && b!="") return -1;
if (a==b) return 0;
integer lA=llStringLength(a);
integer lB=llStringLength(b);
if (!lA && !lB) return 0;
if (lA>lB) return 1;
if (lA<lB) return -1;
integer i=0;
integer ia=0;
integer ib=0;
do
{
ia=(integer)llGetSubString(a,i,(i+8));
ib=(integer)llGetSubString(b,i,(i+8));
if (ia!=ib) jump continue;
i+=9;
} while(i<lA);
@continue;
if (ia>ib) return 1;
if (ia<ib) return -1;
return 0;
}
//****************************************************************
//足し算引き算
//****************************************************************
string longIntSum(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f1==0 && f2==0) return "0";
if (f1!=0 && f2==0) return a;
if (f1==0 && f2!=0) return b;
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return "0";
if (a!="" && b=="")
{
if (f1<0) return "-"+a;
return a;
}
if (a=="" && b!="")
{
if (f2<0) return "-"+b;
return b;
}
integer flag=1;
if (f1!=f2) flag=-1;
integer f3=longIntAbsCmp(a,b);
string rflag="";
if (f3==0 && flag==-1) return "0";
if (f3<0)
{
if (f2<0) rflag="-";
string c=a;
a=b;
b=c;
integer tmp=f2;
f1=f2;
f2=tmp;
}
else
{
if (f1<0) rflag="-";
}
//9ケタづつ加減算
integer lA=llStringLength(a)*-1;
integer lB=llStringLength(b)*-1;
integer k=0;
integer u=0;
string res="";
while(k>lA)
{
k-=9;
integer va=(integer)llGetSubString(a,k,k+8);
va=va+(integer)llGetSubString(b,k,k+8)*flag+u;
u=llFloor((float)va/1000000000.0);
va=llAbs(va-u*1000000000);
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<9)
{
l=8-l;
tmp=llGetSubString("000000000",0,l)+tmp;
}
res=tmp+res;
}
res=rflag+ltrim((string)u+res,"0");
if (res=="") return "0";
if (res=="-") return "0";
return res;
}
//****************************************************************
//掛け算
//****************************************************************
string longIntMul(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f1==0 || f2==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" || b=="") return "0";
if (b=="1")
{
if (f1*f2<0) return "-"+a;
return a;
}
if (a=="1")
{
if (f1*f2<0) return "-"+b;
return b;
}
//3ケタづつ乗算
integer lA=llStringLength(a)*-1;
integer lB=llStringLength(b)*-1;
integer i=0;
integer j=0;
integer k=0;
string res="";
integer of=0;
while(j>lB-3)
{
j-=3;
k=0;
while(k>lA)
{
k-=3;
integer va=(integer)llGetSubString(a,k,k+2);
va=va*(integer)llGetSubString(b,j,j+2)+of*1000000;
of=0;
i=k+j+3;
integer rlen=llStringLength(res);
if (rlen+i<0)
{
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<6)
{
l=5-l;
tmp=llGetSubString("000000",0,l)+tmp;
}
res=tmp+res;
}
else
{
va+=(integer)llGetSubString(res,i-6,i+2);
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<=9)
{
l=9-l;
if (l>0) tmp=llGetSubString("000000000",0,l-1)+tmp;
}
else
{
of=(integer)llGetSubString(tmp,0,l-9-1);
tmp=llGetSubString(tmp,l-9,l);
}
res=llGetSubString(res,rlen*-1+i-7,i-7)+tmp+llGetSubString(res,i+3,-1);
}
}
}
res=ltrim((string)of+res,"0");
if (res=="") return "0";
if (res=="0") return "0";
if (f1*f2>0)
{
return res;
}
else
{
return "-"+res;
}
}
//****************************************************************
//整数の割り算
//****************************************************************
list longIntDiv(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f2==0) return ["INFINITY","0"];
if (f1==0) return ["0",b];
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (b=="") return ["INFINITY","0"];
if (a=="")
{
if (f2<0) return ["0","-"+b];
return ["0",b];
}
//6桁以下の分子なら通常計算して終わる
if (llStringLength(a)<=6)
{
if (longIntAbsCmp(b,a)>0)
{
return ["0",a];
}
else
{
return [llFloor((float)a/(float)b),(integer)a % (integer)b];
}
}
integer lA=llStringLength(a);
integer lB=llStringLength(b);
if (lB>lA) return ["0",a];
if (longIntAbsCmp(a,b)<0) return ["0",a];
integer i=0;
integer j=0;
integer k=0;
string res="";
string mod="0";
string zero="0";
integer B1ToB8=(integer)llGetSubString(b,0,7);
//初期化
string A=llGetSubString(a,0,lB-1);
a=llGetSubString(a,lB,lB+lA);
if (longIntAbsCmp(A,b)<0)
{
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
}
//除算
do
{
integer q=0;
while (!q)
{
integer A1ToA8OrA9=(integer)llGetSubString(A,0,7);
if (llStringLength(A)>7)
{
if (A1ToA8OrA9<B1ToB8)
{
A1ToA8OrA9=A1ToA8OrA9*10+(integer)llGetSubString(A,8,8);
}
}
q=llFloor((float)A1ToA8OrA9/(float)B1ToB8);
if (!q)
{
if (a=="")
{
res=res+zero;
mod=A;
jump continue;
}
res=res+"0";
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
}
}
string bq;
integer test=-1;
while(q>0)
{
if (lB<8)
{
bq=(string)((integer)b*q);
mod=(string)((integer)A-(integer)bq);
test=0;
}
else
{
if (q==1)
{
//仮の商が1。桁が一桁違う場合がありうる。
if (llStringLength(A)>llStringLength(bq))
{
q=10;
while(--q)
{
bq=longIntMul(b,(string)q);
test=longIntAbsCmp(A,bq);
if (test>=0) jump continue3;
}
}
bq=longIntMul(b,(string)q);
@continue3;
}
else
{
bq=longIntMul(b,(string)q);
}
}
if (test==-1) test=longIntAbsCmp(A,bq);
if (test<0)
{
--q;
bq=longIntMul(b,(string)q);
test=longIntAbsCmp(A,bq);
if (test>=0)
{
res=res+(string)q;
jump continue2;
}
}
else
{
res=res+(string)q;
jump continue2;
}
}
@continue2;
if (q<=0)
{
mod=A;
jump continue;
}
zero="";
if (a!="") zero="0";
mod=ltrim(longIntSum(A,"-"+bq),"0");
//次の数字
integer modLen=llStringLength(mod);
A=mod;
if (modLen<lB)
{
integer m=lB-modLen;
integer an=llStringLength(a);
if (an>0)
{
if (m>an) m=an;
while(--m)
{
res=res+"0";
}
m=lB-modLen;
A=A+llGetSubString(a,0,m-1);
a=llGetSubString(a,m,lB+lA);
}
}
if (longIntAbsCmp(A,b)<0)
{
if (a!="")
{
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
if (modLen<lB)
{
res=res+"0";
}
}
else
{
res=res+zero;
jump continue;
}
}
if (llStringLength(A)<lB)
{
res=res+zero;
mod=A;
jump continue;
}
} while(TRUE);
@continue;
res=ltrim(res,"0");
mod=ltrim(mod,"0");
if (mod=="") mod="0";
if (f1*f2<0) res="-"+res;
if (f1<0 && mod!="0") mod="-"+mod;
if (res=="") res="0";
return [res,mod];
}
//****************************************************************
//実数の多倍長加減算
//****************************************************************
string longSum(string a,string b)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f1==0 && f2==0) return "0";
if (f1!=0 && f2==0) return a;
if (f1==0 && f2!=0) return b;
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return "0";
if (a!="" && b=="")
{
if (f1<0) return "-"+a;
return a;
}
if (a=="" && b!="")
{
if (f2<0) return "-"+b;
return b;
}
//準備
//小数点以下が長いほうにあわせて桁移動して整数化。
integer la=llStringLength(a);
integer lb=llStringLength(b);
integer pa=llSubStringIndex(a,".");
integer pb=llSubStringIndex(b,".");
integer digit;
if (pa!=-1 || pb!=-1)
{
if (pa!=la-1 || pb!=lb-1)
{
if (pa==-1)
{
pa=la;
++la;
a=a+".";
}
if (pb==-1)
{
pb=lb;
++lb;
b=b+".";
}
digit=la-pa;
if (lb-pb>digit)
{
digit=lb-pb-digit;
while(digit--)
{
a=a+"0";
}
}
else
{
digit=digit-(lb-pb);
while(digit--)
{
b=b+"0";
}
}
}
a=(string)llParseString2List(a,["."],[]);
b=(string)llParseString2List(b,["."],[]);
}
if (f1<0)
{
a="-"+a;
}
if (f2<0)
{
b="-"+b;
}
string res=longIntSum(a,b);
digit=la-pa;
if (lb-pb>digit)
{
digit=lb-pb;
}
--digit;
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
la=llStringLength(res);
string tmp="";
if (llSubStringIndex(res,"-")==0)
{
tmp="-";
res=llGetSubString(res,1,-1);
--la;
}
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
pa=la-digit;
res=llInsertString(res,pa,".");
}
return tmp+res;
}
//****************************************************************
//実数の多倍長乗算
//****************************************************************
string longMul(string a,string b)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f1==0 || f2==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" || b=="") return "0";
//準備
//小数点以下の長さを記憶しておく。
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
integer digit=llStringLength(a)-llSubStringIndex(a,".")+llStringLength(b)-llSubStringIndex(b,".")-2;
a=(string)llParseString2List(a,["."],[]);
b=(string)llParseString2List(b,["."],[]);
string res=longIntMul(a,b);
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
integer la=llStringLength(res);
if (llSubStringIndex(res,"-")==0)
{
res=llGetSubString(res,1,-1);
--la;
}
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
integer pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
integer pa=la-digit;
res=llInsertString(res,pa,".");
}
if (f1*f2>0)
{
return res;
}
else
{
return "-"+res;
}
}
//****************************************************************
//実数の多倍長割り算
//第一引数:分子(被除数)
//第二引数:分母(除数)
//第3引数は小数点以下の桁数を指定
//****************************************************************
string longDiv(string a, string b,integer digit)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f2==0) return "INFINITY";
if (f1==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (b=="") return "INFINITY";
if (a=="") return "0";
//準備 / 分子分母の整数化
integer pa=llSubStringIndex(a,".");
integer la=llStringLength(a);
if (pa==0)
{
a="0"+a;
pa=1;
++la;
}
if (pa==-1)
{
pa=la;
a=a+".";
++la;
}
integer pb=llSubStringIndex(b,".");
integer lb=llStringLength(b);
if (pb==-1)
{
pb=lb;
++lb;
}
else if (pb==0)
{
pb=1;
++lb;
}
//分子小数点以下に希望の桁数を追加
integer i=digit-(lb-pb-1);
if (i<0)
{
//小数点以下が長すぎる
b=llGetSubString(b,0,pb+digit);
lb=llStringLength(b);
pb=llSubStringIndex(b,".");
}
i=digit-(la-pa-1);
if (i<0)
{
//小数点以下が長すぎる
i=0;
a=llGetSubString(a,0,pa+digit);
la=llStringLength(a);
pa=llSubStringIndex(a,".");
}
if (la-pa<lb-pb) i=i+lb-pb-la+pa;
while(i--)
{
a=a+"0";
}
if (pb>=0)
{
//分母に小数点。
//分母を整数にし、分子の小数点を移動
b=(string)llParseString2List(b,["."],[]);
integer p=lb-pb-1;
string floatA=llGetSubString(a,pa+1,-1);
a=llGetSubString(a,0,pa-1)+llInsertString(floatA,p,".");
}
//桁数の補正
//digitより小数点以下の数が少なければ追加
pa=digit-(llStringLength(a)-llSubStringIndex(a,".")-1);
if (pa>0)
{
do
{
a=a+"0";
}while(--pa);
}
a=(string)llParseString2List(a,["."],[]);
//計算実行
string res=llList2String(longIntDiv(a,b),0);
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
la=llStringLength(res);
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
pa=la-digit;
res=llInsertString(res,pa,".");
}
if (f1*f2<0) res="-"+res;
return res;
}
//****************************************************************
//多倍長計算関連おしまい
//****************************************************************
default
{
state_entry()
{
llResetTime();
llOwnerSay(longSum("-0.0960866054","-0.0452746054"));
llOwnerSay((string)llGetTime());
llResetTime();
llOwnerSay(longMul("0.0960866054","-1.0452746054"));
llOwnerSay((string)llGetTime());
llResetTime();
llOwnerSay(longDiv("2304.0960866054","0.0452746054",20));
llOwnerSay((string)llGetTime());
}
}
負数に対応しています(はずです。。。(笑))。
以下アルゴリズムです。
検索から飛んで来られる方がおられるようですが、こちらは32ビット符号付整数と(バグがあるとかないとか言う)単精度浮動小数点数しかないLSLという環境用です。乗算や除算には、メモリーが許せばもっと高速なアルゴリズムがあったと思います。
1:足し算引き算
筆算と同じです。9桁づつ文字列から取り出して計算し、繰上げ切り下げを次の桁で行います。
2:掛け算
筆算と同じです。3桁づつ文字列から取り出して計算し、9桁までの繰上げはその場で、10桁以降は次の桁計算に持ち越します。
3:割り算
筆算と同じです。ただし商を求める際に分母先頭8桁と分子先頭8桁を使って仮の商を算出し、手順を簡略化しています。
整数の割り算(longIntDiv())のみ、listが戻りになり、0番が商、1番が剰余になります。
longDiv()では戻りは商のみとなります。
2010/4/28:追記および変更
サンプルを削除しました。
バグを修正し、実数計算を追加しました。
小数点を一旦消して整数計算して戻しているだけですが、高次の連立方程式用として現在試験中です。
桁数の管理や精度はかなりいい加減です。加減乗算では小数点以下の桁数を管理しておらず、割り算では桁数が多すぎると無条件に切り捨てていますので。。。^^;
また、いちいち文字列から部分を抜き出していますが、あらかじめlistに桁あふれしない長さの整数で格納しておくほうが高速に動作するはずです。(listはメモリー的に不利ですから。。。)
サンプルを削除しました。
バグを修正し、実数計算を追加しました。
小数点を一旦消して整数計算して戻しているだけですが、高次の連立方程式用として現在試験中です。
桁数の管理や精度はかなりいい加減です。加減乗算では小数点以下の桁数を管理しておらず、割り算では桁数が多すぎると無条件に切り捨てていますので。。。^^;
また、いちいち文字列から部分を抜き出していますが、あらかじめlistに桁あふれしない長さの整数で格納しておくほうが高速に動作するはずです。(listはメモリー的に不利ですから。。。)
// www.lsleditor.org by Alphons van der Heijden (SL: Alphons Jano)
//****************************************************************
//多倍長実数計算
//****************************************************************
//整数であるか調べ、符号かFALSEを返す
integer isInt(string s)
{
list l=["0","1","2","3","4","5","6","7","8","9","-"];
integer i=llStringLength(s);
if (!i) return FALSE;
if (s=="0") return FALSE;
if (s=="-0") return FALSE;
if (s=="-") return FALSE;
do
{
--i;
if (llListFindList(l,[llGetSubString(s,i,i)])<0) return FALSE;
} while (i);
if (llSubStringIndex(s,"-")==0) return -1;
return 1;
}
//実数であるか調べ、符号かFALSEを返す
integer isFloat(string s)
{
list l=["0","1","2","3","4","5","6","7","8","9","-","."];
integer i=llStringLength(s);
if (!i) return FALSE;
if (s=="0") return FALSE;
if (s=="-0") return FALSE;
if (s=="-") return FALSE;
do
{
--i;
if (llListFindList(l,[llGetSubString(s,i,i)])<0) return FALSE;
} while (i);
if (llSubStringIndex(s,"-")==0) return -1;
return 1;
}
//文字列先頭の指定文字を削除
string ltrim(string s, string t)
{
if (llGetSubString(s,0,0)!=t) return s;
integer i=0;
integer maxI=llStringLength(s);
if (!maxI) return s;
++maxI;
while(i<maxI)
{
++i;
if (llGetSubString(s,i,i)!=t) jump continue;
}
@continue;
return llGetSubString(s,i,maxI);
}
//文字列末尾の指定文字を削除
string rtrim(string s, string t)
{
if (llGetSubString(s,-1,-1)!=t) return s;
integer i=llStringLength(s);
if (!i) return s;
while(i--)
{
if (llGetSubString(s,i,i)!=t) jump continue;
}
@continue;
return llGetSubString(s,0,i);
}
//整数数値文字列の絶対値について大小比較
integer longIntAbsCmp(string a, string b)
{
a=ltrim(a,"-");
b=ltrim(b,"-");
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return 0;
if (a!="" && b=="") return 1;
if (a=="" && b!="") return -1;
if (a==b) return 0;
integer lA=llStringLength(a);
integer lB=llStringLength(b);
if (!lA && !lB) return 0;
if (lA>lB) return 1;
if (lA<lB) return -1;
integer i=0;
integer ia=0;
integer ib=0;
do
{
ia=(integer)llGetSubString(a,i,(i+8));
ib=(integer)llGetSubString(b,i,(i+8));
if (ia!=ib) jump continue;
i+=9;
} while(i<lA);
@continue;
if (ia>ib) return 1;
if (ia<ib) return -1;
return 0;
}
//****************************************************************
//足し算引き算
//****************************************************************
string longIntSum(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f1==0 && f2==0) return "0";
if (f1!=0 && f2==0) return a;
if (f1==0 && f2!=0) return b;
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return "0";
if (a!="" && b=="")
{
if (f1<0) return "-"+a;
return a;
}
if (a=="" && b!="")
{
if (f2<0) return "-"+b;
return b;
}
integer flag=1;
if (f1!=f2) flag=-1;
integer f3=longIntAbsCmp(a,b);
string rflag="";
if (f3==0 && flag==-1) return "0";
if (f3<0)
{
if (f2<0) rflag="-";
string c=a;
a=b;
b=c;
integer tmp=f2;
f1=f2;
f2=tmp;
}
else
{
if (f1<0) rflag="-";
}
//9ケタづつ加減算
integer lA=llStringLength(a)*-1;
integer lB=llStringLength(b)*-1;
integer k=0;
integer u=0;
string res="";
while(k>lA)
{
k-=9;
integer va=(integer)llGetSubString(a,k,k+8);
va=va+(integer)llGetSubString(b,k,k+8)*flag+u;
u=llFloor((float)va/1000000000.0);
va=llAbs(va-u*1000000000);
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<9)
{
l=8-l;
tmp=llGetSubString("000000000",0,l)+tmp;
}
res=tmp+res;
}
res=rflag+ltrim((string)u+res,"0");
if (res=="") return "0";
if (res=="-") return "0";
return res;
}
//****************************************************************
//掛け算
//****************************************************************
string longIntMul(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f1==0 || f2==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" || b=="") return "0";
if (b=="1")
{
if (f1*f2<0) return "-"+a;
return a;
}
if (a=="1")
{
if (f1*f2<0) return "-"+b;
return b;
}
//3ケタづつ乗算
integer lA=llStringLength(a)*-1;
integer lB=llStringLength(b)*-1;
integer i=0;
integer j=0;
integer k=0;
string res="";
integer of=0;
while(j>lB-3)
{
j-=3;
k=0;
while(k>lA)
{
k-=3;
integer va=(integer)llGetSubString(a,k,k+2);
va=va*(integer)llGetSubString(b,j,j+2)+of*1000000;
of=0;
i=k+j+3;
integer rlen=llStringLength(res);
if (rlen+i<0)
{
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<6)
{
l=5-l;
tmp=llGetSubString("000000",0,l)+tmp;
}
res=tmp+res;
}
else
{
va+=(integer)llGetSubString(res,i-6,i+2);
string tmp=(string)va;
integer l=llStringLength(tmp);
if (l<=9)
{
l=9-l;
if (l>0) tmp=llGetSubString("000000000",0,l-1)+tmp;
}
else
{
of=(integer)llGetSubString(tmp,0,l-9-1);
tmp=llGetSubString(tmp,l-9,l);
}
res=llGetSubString(res,rlen*-1+i-7,i-7)+tmp+llGetSubString(res,i+3,-1);
}
}
}
res=ltrim((string)of+res,"0");
if (res=="") return "0";
if (res=="0") return "0";
if (f1*f2>0)
{
return res;
}
else
{
return "-"+res;
}
}
//****************************************************************
//整数の割り算
//****************************************************************
list longIntDiv(string a, string b)
{
integer f1=isInt(a);
integer f2=isInt(b);
if (f2==0) return ["INFINITY","0"];
if (f1==0) return ["0",b];
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (b=="") return ["INFINITY","0"];
if (a=="")
{
if (f2<0) return ["0","-"+b];
return ["0",b];
}
//6桁以下の分子なら通常計算して終わる
if (llStringLength(a)<=6)
{
if (longIntAbsCmp(b,a)>0)
{
return ["0",a];
}
else
{
return [llFloor((float)a/(float)b),(integer)a % (integer)b];
}
}
integer lA=llStringLength(a);
integer lB=llStringLength(b);
if (lB>lA) return ["0",a];
if (longIntAbsCmp(a,b)<0) return ["0",a];
integer i=0;
integer j=0;
integer k=0;
string res="";
string mod="0";
string zero="0";
integer B1ToB8=(integer)llGetSubString(b,0,7);
//初期化
string A=llGetSubString(a,0,lB-1);
a=llGetSubString(a,lB,lB+lA);
if (longIntAbsCmp(A,b)<0)
{
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
}
//除算
do
{
integer q=0;
while (!q)
{
integer A1ToA8OrA9=(integer)llGetSubString(A,0,7);
if (llStringLength(A)>7)
{
if (A1ToA8OrA9<B1ToB8)
{
A1ToA8OrA9=A1ToA8OrA9*10+(integer)llGetSubString(A,8,8);
}
}
q=llFloor((float)A1ToA8OrA9/(float)B1ToB8);
if (!q)
{
if (a=="")
{
res=res+zero;
mod=A;
jump continue;
}
res=res+"0";
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
}
}
string bq;
integer test=-1;
while(q>0)
{
if (lB<8)
{
bq=(string)((integer)b*q);
mod=(string)((integer)A-(integer)bq);
test=0;
}
else
{
if (q==1)
{
//仮の商が1。桁が一桁違う場合がありうる。
if (llStringLength(A)>llStringLength(bq))
{
q=10;
while(--q)
{
bq=longIntMul(b,(string)q);
test=longIntAbsCmp(A,bq);
if (test>=0) jump continue3;
}
}
bq=longIntMul(b,(string)q);
@continue3;
}
else
{
bq=longIntMul(b,(string)q);
}
}
if (test==-1) test=longIntAbsCmp(A,bq);
if (test<0)
{
--q;
bq=longIntMul(b,(string)q);
test=longIntAbsCmp(A,bq);
if (test>=0)
{
res=res+(string)q;
jump continue2;
}
}
else
{
res=res+(string)q;
jump continue2;
}
}
@continue2;
if (q<=0)
{
mod=A;
jump continue;
}
zero="";
if (a!="") zero="0";
mod=ltrim(longIntSum(A,"-"+bq),"0");
//次の数字
integer modLen=llStringLength(mod);
A=mod;
if (modLen<lB)
{
integer m=lB-modLen;
integer an=llStringLength(a);
if (an>0)
{
if (m>an) m=an;
while(--m)
{
res=res+"0";
}
m=lB-modLen;
A=A+llGetSubString(a,0,m-1);
a=llGetSubString(a,m,lB+lA);
}
}
if (longIntAbsCmp(A,b)<0)
{
if (a!="")
{
A=A+llGetSubString(a,0,0);
a=llGetSubString(a,1,lB+lA);
if (modLen<lB)
{
res=res+"0";
}
}
else
{
res=res+zero;
jump continue;
}
}
if (llStringLength(A)<lB)
{
res=res+zero;
mod=A;
jump continue;
}
} while(TRUE);
@continue;
res=ltrim(res,"0");
mod=ltrim(mod,"0");
if (mod=="") mod="0";
if (f1*f2<0) res="-"+res;
if (f1<0 && mod!="0") mod="-"+mod;
if (res=="") res="0";
return [res,mod];
}
//****************************************************************
//実数の多倍長加減算
//****************************************************************
string longSum(string a,string b)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f1==0 && f2==0) return "0";
if (f1!=0 && f2==0) return a;
if (f1==0 && f2!=0) return b;
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" && b=="") return "0";
if (a!="" && b=="")
{
if (f1<0) return "-"+a;
return a;
}
if (a=="" && b!="")
{
if (f2<0) return "-"+b;
return b;
}
//準備
//小数点以下が長いほうにあわせて桁移動して整数化。
integer la=llStringLength(a);
integer lb=llStringLength(b);
integer pa=llSubStringIndex(a,".");
integer pb=llSubStringIndex(b,".");
integer digit;
if (pa!=-1 || pb!=-1)
{
if (pa!=la-1 || pb!=lb-1)
{
if (pa==-1)
{
pa=la;
++la;
a=a+".";
}
if (pb==-1)
{
pb=lb;
++lb;
b=b+".";
}
digit=la-pa;
if (lb-pb>digit)
{
digit=lb-pb-digit;
while(digit--)
{
a=a+"0";
}
}
else
{
digit=digit-(lb-pb);
while(digit--)
{
b=b+"0";
}
}
}
a=(string)llParseString2List(a,["."],[]);
b=(string)llParseString2List(b,["."],[]);
}
if (f1<0)
{
a="-"+a;
}
if (f2<0)
{
b="-"+b;
}
string res=longIntSum(a,b);
digit=la-pa;
if (lb-pb>digit)
{
digit=lb-pb;
}
--digit;
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
la=llStringLength(res);
string tmp="";
if (llSubStringIndex(res,"-")==0)
{
tmp="-";
res=llGetSubString(res,1,-1);
--la;
}
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
pa=la-digit;
res=llInsertString(res,pa,".");
}
return tmp+res;
}
//****************************************************************
//実数の多倍長乗算
//****************************************************************
string longMul(string a,string b)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f1==0 || f2==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (a=="" || b=="") return "0";
//準備
//小数点以下の長さを記憶しておく。
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
integer digit=llStringLength(a)-llSubStringIndex(a,".")+llStringLength(b)-llSubStringIndex(b,".")-2;
a=(string)llParseString2List(a,["."],[]);
b=(string)llParseString2List(b,["."],[]);
string res=longIntMul(a,b);
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
integer la=llStringLength(res);
if (llSubStringIndex(res,"-")==0)
{
res=llGetSubString(res,1,-1);
--la;
}
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
integer pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
integer pa=la-digit;
res=llInsertString(res,pa,".");
}
if (f1*f2>0)
{
return res;
}
else
{
return "-"+res;
}
}
//****************************************************************
//実数の多倍長割り算
//第一引数:分子(被除数)
//第二引数:分母(除数)
//第3引数は小数点以下の桁数を指定
//****************************************************************
string longDiv(string a, string b,integer digit)
{
if (llSubStringIndex(a,".")==-1) a=a+".";
if (llSubStringIndex(b,".")==-1) b=b+".";
a=rtrim(a,"0");
b=rtrim(b,"0");
integer f1=isFloat(a);
integer f2=isFloat(b);
if (f2==0) return "INFINITY";
if (f1==0) return "0";
if (f1<0)
{
a=llGetSubString(a,1,-1);
}
if (f2<0)
{
b=llGetSubString(b,1,-1);
}
a=ltrim(a,"0");
b=ltrim(b,"0");
if (b=="") return "INFINITY";
if (a=="") return "0";
//準備 / 分子分母の整数化
integer pa=llSubStringIndex(a,".");
integer la=llStringLength(a);
if (pa==0)
{
a="0"+a;
pa=1;
++la;
}
if (pa==-1)
{
pa=la;
a=a+".";
++la;
}
integer pb=llSubStringIndex(b,".");
integer lb=llStringLength(b);
if (pb==-1)
{
pb=lb;
++lb;
}
else if (pb==0)
{
pb=1;
++lb;
}
//分子小数点以下に希望の桁数を追加
integer i=digit-(lb-pb-1);
if (i<0)
{
//小数点以下が長すぎる
b=llGetSubString(b,0,pb+digit);
lb=llStringLength(b);
pb=llSubStringIndex(b,".");
}
i=digit-(la-pa-1);
if (i<0)
{
//小数点以下が長すぎる
i=0;
a=llGetSubString(a,0,pa+digit);
la=llStringLength(a);
pa=llSubStringIndex(a,".");
}
if (la-pa<lb-pb) i=i+lb-pb-la+pa;
while(i--)
{
a=a+"0";
}
if (pb>=0)
{
//分母に小数点。
//分母を整数にし、分子の小数点を移動
b=(string)llParseString2List(b,["."],[]);
integer p=lb-pb-1;
string floatA=llGetSubString(a,pa+1,-1);
a=llGetSubString(a,0,pa-1)+llInsertString(floatA,p,".");
}
//桁数の補正
//digitより小数点以下の数が少なければ追加
pa=digit-(llStringLength(a)-llSubStringIndex(a,".")-1);
if (pa>0)
{
do
{
a=a+"0";
}while(--pa);
}
a=(string)llParseString2List(a,["."],[]);
//計算実行
string res=llList2String(longIntDiv(a,b),0);
//戻り作成
//戻りの桁数がdigitより小さい場合冒頭に0.000・・・を追加
la=llStringLength(res);
if (la==digit)
{
res="0."+res;
}
else if (la<digit)
{
pa=digit-la;
while(pa--)
{
res="0"+res;
}
res="0."+res;
}
else
{
pa=la-digit;
res=llInsertString(res,pa,".");
}
if (f1*f2<0) res="-"+res;
return res;
}
//****************************************************************
//多倍長計算関連おしまい
//****************************************************************
default
{
state_entry()
{
llResetTime();
llOwnerSay(longSum("-0.0960866054","-0.0452746054"));
llOwnerSay((string)llGetTime());
llResetTime();
llOwnerSay(longMul("0.0960866054","-1.0452746054"));
llOwnerSay((string)llGetTime());
llResetTime();
llOwnerSay(longDiv("2304.0960866054","0.0452746054",20));
llOwnerSay((string)llGetTime());
}
}
2009年12月04日
lsl 特定の面のサイズと4隅のリージョン座標を取得する
あってしかるべき物の様な気もするのですが、見つからなかったので作りました。
手計算すれば求まりますが、テーパーが入った上に上部が入っていたり、形状がややこしいと私のように計算に弱い頭は、すぐにところてんになってしまいますので、タッチイベントで取得できるタッチ位置のリージョン座標と、面上のST座標を利用して数値計算で割り出すことにします。(といいますか代換手段がみつかるまでは一度作ってしまえば楽ができますので。。。(笑))
タッチされた面上のST座標は単純にプリムにマス目テクスチャを貼り付けたときの歪みと一致している様で、下の画像の様に左下と右上を結ぶ対角線を境にして座標系が折れ曲がっています。(白線がその対角線)

このとき、

のような図を考えますと、llDetectedTouchST()関数で取得できる面上の座標(S,T)は、対角線の下半分(青色の部分)で、Sは下底に平行、Tは右辺に平行に値が変化しますので、結局、タッチした点PのリージョンベクトルVPは、
VP=V0+HR*T+WB*S
となります。
未知数(未知ベクトル?)がV0、HR、WBの3つですので、青色部分の範囲内で3点をタッチして連立方程式にすれば、これらの情報は求まります。
VP1=V0+HR*T1+WB*S1
VP2=V0+HR*T2+WB*S2
VP3=V0+HR*T3+WB*S3
この連立方程式は展開してもベクトルの割り算を含みませんので、幸いなことに高校数学程度の知識でも解く事が出来ました。^^;
平行四辺形と三角形はこれで全て算出できますが、上図のような任意の四角形の場合には対角線より上のもう一点をタッチし、同じように左辺と上底の関係で現した式に入れれば求まることになります。
3点タッチの時点で3頂点に関する情報が求まっていますので、4点目はただの代入になります。
VTL=(P4-S4*VRT-(1-T4)*V0)/(T4-S4)
末尾は3点・4点タッチでグローバル変数に計算結果を入れるサンプルスクリプトです。
式の展開結果は、http://www.usamimi.info/~geko/arch_acade/elf001_simult/index.htmlを検索していて見つけました。利用させていただきました。
手計算すれば求まりますが、テーパーが入った上に上部が入っていたり、形状がややこしいと私のように計算に弱い頭は、すぐにところてんになってしまいますので、タッチイベントで取得できるタッチ位置のリージョン座標と、面上のST座標を利用して数値計算で割り出すことにします。(といいますか代換手段がみつかるまでは一度作ってしまえば楽ができますので。。。(笑))
タッチされた面上のST座標は単純にプリムにマス目テクスチャを貼り付けたときの歪みと一致している様で、下の画像の様に左下と右上を結ぶ対角線を境にして座標系が折れ曲がっています。(白線がその対角線)

このとき、

のような図を考えますと、llDetectedTouchST()関数で取得できる面上の座標(S,T)は、対角線の下半分(青色の部分)で、Sは下底に平行、Tは右辺に平行に値が変化しますので、結局、タッチした点PのリージョンベクトルVPは、
VP=V0+HR*T+WB*S
となります。
未知数(未知ベクトル?)がV0、HR、WBの3つですので、青色部分の範囲内で3点をタッチして連立方程式にすれば、これらの情報は求まります。
VP1=V0+HR*T1+WB*S1
VP2=V0+HR*T2+WB*S2
VP3=V0+HR*T3+WB*S3
この連立方程式は展開してもベクトルの割り算を含みませんので、幸いなことに高校数学程度の知識でも解く事が出来ました。^^;
平行四辺形と三角形はこれで全て算出できますが、上図のような任意の四角形の場合には対角線より上のもう一点をタッチし、同じように左辺と上底の関係で現した式に入れれば求まることになります。
3点タッチの時点で3頂点に関する情報が求まっていますので、4点目はただの代入になります。
VTL=(P4-S4*VRT-(1-T4)*V0)/(T4-S4)
末尾は3点・4点タッチでグローバル変数に計算結果を入れるサンプルスクリプトです。
式の展開結果は、http://www.usamimi.info/~geko/arch_acade/elf001_simult/index.htmlを検索していて見つけました。利用させていただきました。
// www.lsleditor.org by Alphons van der Heijden (SL: Alphons Jano)
//*****************************************************************************************
//メッセージ類
//*****************************************************************************************
string ERR_TOO_NEAR="";
setTextMessage()
{
if (llGetAgentLanguage(llGetOwner())=="ja")
{
//日本語
ERR_TOO_NEAR="選択した点が近すぎます";
}
else
{
//その他
ERR_TOO_NEAR="The touched point is too near.";
}
}
//*****************************************************************************************
//初期化
//*****************************************************************************************
vector E1=ZERO_VECTOR;
vector E2=ZERO_VECTOR;
vector E3=ZERO_VECTOR;
vector E4=ZERO_VECTOR;
vector ST1=ZERO_VECTOR;
vector ST2=ZERO_VECTOR;
vector ST3=ZERO_VECTOR;
vector ST4=ZERO_VECTOR;
integer face1=-1;
integer face2=-2;
integer face3=-3;
integer face4=-4;
vector V0;
vector VRT;
vector VLT;
vector HL;
vector HR;
vector WT;
vector WB;
init()
{
setTextMessage();
}
default
{
state_entry()
{
init();
}
touch_start(integer total_number)
{
face4=llDetectedTouchFace(0);
E4=llDetectedTouchPos(0);
ST4=llDetectedTouchST(0);
if (face1!=face4)
{
if (llVecDist(E3,E4)<0.05 || llVecDist(E2,E4)<0.05)
{
llOwnerSay(ERR_TOO_NEAR);
face1=-1;
face2=-2;
face3=-3;
face4=-4;
E1=ZERO_VECTOR;
E2=ZERO_VECTOR;
E3=ZERO_VECTOR;
E4=ZERO_VECTOR;
return;
}
face2=-2;
face3=-3;
face1=face4;
E1=E4;
ST1=ST4;
return;
}
else if (face2!=face4)
{
if (llVecDist(E1,E4)<0.05 || llVecDist(E3,E4)<0.05)
{
llOwnerSay(ERR_TOO_NEAR);
face1=-1;
face2=-2;
face3=-3;
face4=-4;
E1=ZERO_VECTOR;
E2=ZERO_VECTOR;
E3=ZERO_VECTOR;
E4=ZERO_VECTOR;
return;
}
face2=face4;
E2=E4;
ST2=ST4;
return;
}
else if (face3!=face4)
{
if (llVecDist(E1,E4)<0.05 || llVecDist(E2,E4)<0.05)
{
llOwnerSay(ERR_TOO_NEAR);
face1=-1;
face2=-2;
face3=-3;
face4=-4;
E1=ZERO_VECTOR;
E2=ZERO_VECTOR;
E3=ZERO_VECTOR;
E4=ZERO_VECTOR;
return;
}
face3=face4;
E3=E4;
ST3=ST4;
float A1=1.0;
float A2=1.0;
float A3=1.0;
float B1=ST1.y;
float B2=ST2.y;
float B3=ST3.y;
float C1=ST1.x;
float C2=ST2.x;
float C3=ST3.x;
//座標原点(左下)
V0=(E1*B2*C3+E2*B3*C1+E3*B1*C2-E1*B3*C2-E2*B1*C3-E3*B2*C1)/(A1*B2*C3+A2*B3*C1+A3*B1*C2-A1*B3*C2-A2*B1*C3-A3*B2*C1);
//下底ベクトル
WB=(A1*B2*E3+A2*B3*E1+A3*B1*E2-A1*B3*E2-A2*B1*E3-A3*B2*E1)/(A1*B2*C3+A2*B3*C1+A3*B1*C2-A1*B3*C2-A2*B1*C3-A3*B2*C1);
//右辺ベクトル
HR=(A1*E2*C3+A2*E3*C1+A3*E1*C2-A1*E3*C2-A2*E1*C3-A3*E2*C1)/(A1*B2*C3+A2*B3*C1+A3*B1*C2-A1*B3*C2-A2*B1*C3-A3*B2*C1);
//座標最大点(右上)
VRT=V0+WB+HR;
}
else
{
if (llVecDist(E1,E4)<0.05 || llVecDist(E2,E4)<0.05 || llVecDist(E3,E4)<0.05)
{
llOwnerSay(ERR_TOO_NEAR);
face1=-1;
face2=-2;
face3=-3;
face4=-4;
E1=ZERO_VECTOR;
E2=ZERO_VECTOR;
E3=ZERO_VECTOR;
E4=ZERO_VECTOR;
return;
}
//左辺上の頂点
VLT=(E4-ST4.x*VRT-(1.0-ST4.y)*V0)/(ST4.y-ST4.x);
//左辺ベクトル
HL=VLT-V0;
//上辺ベクトル
WT=VRT-VLT;
face1=-1;
face2=-2;
face3=-3;
face4=-4;
E1=ZERO_VECTOR;
E2=ZERO_VECTOR;
E3=ZERO_VECTOR;
E4=ZERO_VECTOR;
}
}
}
2009年11月03日
lsl 座標系の変換(vector)
取得したリージョン座標から子プリムのローカル座標への変換がしたかったので作ってみました。
仕組みは割と簡単ですが、相変わらず我流です。
本当はもう少しいい方法があるのかもしれません。
1:親座標と子座標の差分を取って、リージョンX軸との回転を割り出す
2:親の回転による正面方向のベクトルとリージョンX軸との回転を割り出す
3:1の回転を2の回転で割り、その回転の正面方向のベクトルを取る(座標系の変換)
4:1の差分ベクトルの長さを3に掛ける
末尾は関数化したものです。
それはそうと、お知り合いのTwinker TellingさんがついにSIMを購入されました。
11月1日からグランドオープンで、現在はオープン記念にモール内などにいろいろなクリエイター様の記念フリーアイテムがおいてあります。11月8日夜22:00からはダンスイベントもあるそうです。
動画は初日のダンスイベントの様子をreisei Genesisさんが編集されたものです。
http://slurl.com/secondlife/ArtsStyle/74/97/301

ロサンゼルスの風景を模したSIMデザインはRocket Biedermannさん&Lieza Noelさんによるもの。今はダンスイベントの会場となっていて自由には走れませんが、広々とした道路は快適なドライブを楽しめます。

仕組みは割と簡単ですが、相変わらず我流です。
本当はもう少しいい方法があるのかもしれません。
1:親座標と子座標の差分を取って、リージョンX軸との回転を割り出す
2:親の回転による正面方向のベクトルとリージョンX軸との回転を割り出す
3:1の回転を2の回転で割り、その回転の正面方向のベクトルを取る(座標系の変換)
4:1の差分ベクトルの長さを3に掛ける
末尾は関数化したものです。
それはそうと、お知り合いのTwinker TellingさんがついにSIMを購入されました。
11月1日からグランドオープンで、現在はオープン記念にモール内などにいろいろなクリエイター様の記念フリーアイテムがおいてあります。11月8日夜22:00からはダンスイベントもあるそうです。
動画は初日のダンスイベントの様子をreisei Genesisさんが編集されたものです。
http://slurl.com/secondlife/ArtsStyle/74/97/301

ロサンゼルスの風景を模したSIMデザインはRocket Biedermannさん&Lieza Noelさんによるもの。今はダンスイベントの会場となっていて自由には走れませんが、広々とした道路は快適なドライブを楽しめます。

//リージョン座標系の座標差分からローカル座標へ変換
//vector regionDeltaVec2LocalVec(vector リージョン座標でのルートと子プリムの座標差分 , ルートの回転)
//戻り
//vector ローカル座標系で表現したルートと子プリムの座標差分(≒そのままローカル座標)
vector regionDeltaVec2LocalVec(vector dVec,rotation rootRot)
{
if (dVec==ZERO_VECTOR) return dVec;
if (rootRot==ZERO_ROTATION) return dVec;
//リージョン座標系の差分が向いている方向
rotation rot=llRotBetween(<1.0,0.0,0.0>,dVec);
//長さ
float R=llVecMag(dVec);
//現在のルートローテーションによる座標系の正面方向
rotation fwdRot=llRotBetween(<1.0,0.0,0.0>,llRot2Fwd(rootRot));
//座標系の回転を相殺した後の正面方向
vector newFwd=llRot2Fwd(rot/fwdRot);
return newFwd*R;
}
2009年08月08日
スカート製造装置(物体の回転その3)
 既製品スカートの構造を見るとつまり対空砲でしたので、楕円軌道上に展開するスカート製造装置をつくってみました。
既製品スカートの構造を見るとつまり対空砲でしたので、楕円軌道上に展開するスカート製造装置をつくってみました。楕円の方程式は
x*x/a*a-y*y/b*b=1
y=tan(θ)*x
を代入して変形すると、
(1/a/a+tan(θ)*tan(θ)/b/b)x*x-1=0
となり、あとは二次方程式の根の公式なり、手計算変形なりで部品をrezすべきy座標はみつかります。
それに対空砲を組み合わせてやれば、スカートは自動で製造出来るということになります。
多少アレンジして設定ファイルを読み込むようにしました。
本体が入っているオブジェクトの中にsettingsがあり、本体のインベントリにスカートの部品をいれると準備が完了します。あとはタッチで。
本体
//90度を何分割するか
integer maxNumOfPartitions=10;
//楕円のX軸方向の半径(メートル)
float a=0.25;
//楕円のY軸方向の半径(メートル)
float b=0.2;
//ひらひらの縦方向の傾き(度)。プラス指定で上がすぼまる
float ThetaZ=10;
//スカートを出現させる位置の装置中心からのX軸距離
float offsetX=0.0;
//スカートを出現させる位置の装置中心からのY軸距離
float offsetY=0.0;
//スカートを出現させる装置中心位置からの高さ調整
float offsetZ=0.5;
//X平面から離れていく大きさ
float dXZ=0;
//X平面から離れていく大きさ
float dYZ=0;
float x1=0.0;
float y1=0.0;
float dTheta=PI;
float Theta=0;
string partsName="";
key settingsHandle;
integer settingsLine;
list objectNames_Inventory=[];
integer isReading=FALSE;
integer isMaking=FALSE;
init()
{
Theta=0;
//設定読み込み
readConf();
//向き直る
llSetRot(ZERO_ROTATION);
}
readConf()
{
//設定のノートカード読み取り
isReading=TRUE;
settingsLine=0;
settingsHandle=llGetNotecardLine("settings",settingsLine);
}
remveObject()
{
//インベントリー内部掃除
integer num=llGetInventoryNumber(INVENTORY_OBJECT);
integer i=0;
if (num!=INVENTORY_NONE)
{
for (i=0;i<num;i++)
{
llRemoveInventory(llGetInventoryName(INVENTORY_OBJECT,0));
}
}
}
setPoint()
{
if (llFabs(Theta)==PI/2)
{
y1=b;
}
else
{
y1=llSqrt((1-x1*x1/a/a)*b*b);
}
}
rezOb(float x,float y)
{
vector targetVec=<x,y,0>;
vector norm=llVecNorm(targetVec);
rotation newRot=llRotBetween(<1,0,0>,<norm.x,norm.y,0>);
rotation newRot2=llEuler2Rot(<0,PI+ThetaZ*DEG_TO_RAD*-1.0,0>);
if (partsName!="" && llGetInventoryKey(partsName)!=NULL_KEY)
{
llRezObject(partsName,llGetRootPosition()+<x+offsetX,y+offsetY,offsetZ*-1-x*llSin(dXZ*DEG_TO_RAD)-y*llSin(dYZ*DEG_TO_RAD)>,ZERO_VECTOR,newRot2*newRot,1);
}
}
rezObject()
{
setPoint();
rezOb(x1,y1);
rezOb(x1*-1,y1);
rezOb(x1,y1*-1);
rezOb(x1*-1,y1*-1);
}
default
{
state_entry()
{
init();
remveObject();
}
on_rez(integer start_param)
{
init();
remveObject();
}
touch_start(integer total_number)
{
if (isMaking)
{
llSay(0,"Ooops! Now,I'm busy.Please wait a moment");
return;
}
llSay(0,"Start create a new skirt");
if (partsName=="" || llGetInventoryKey(partsName)==NULL_KEY)
{
llOwnerSay("ERROR:I can't find prim "+partsName+" in my inventory.");
return;
}
isMaking=TRUE;
init();
llSetTimerEvent(0.1);
}
timer()
{
if (isReading)
{
return;
}
llSetTimerEvent(0.0);
integer i=0;
float CA=0;
float CB=0;
float CC=-1;
rezOb(a,0);
rezOb(a*-1,0);
rezOb(0,b);
rezOb(0,b*-1);
for (i=1;i<maxNumOfPartitions;i++)
{
Theta=dTheta*i;
CA=1/a/a+llTan(Theta)*llTan(Theta)/b/b;
x1=(llSqrt(CB*CB-4*CA*CC)-CB)/(2*CA);
rezObject();
}
llSleep(2.0);
llSay(0,"Finished");
isMaking=FALSE;
}
changed(integer change)
{
integer num=llGetListLength(objectNames_Inventory);
integer num2=llGetInventoryNumber(INVENTORY_OBJECT);
integer i=0;
string objName="";
integer j=-1;
list tmp=[];
if (change & CHANGED_INVENTORY)
{
if (num2>0)
{
for (i=0;i<num2;i++)
{
objName=llGetInventoryName(INVENTORY_OBJECT,i);
tmp+=objName;
j=llListFindList(objectNames_Inventory,[objName]);
if (j==-1)
{
partsName=objName;
llOwnerSay("Found new item:"+partsName);
}
}
}
else
{
partsName="";
}
objectNames_Inventory=tmp;
}
}
dataserver(key requested, string data)
{
integer p=-1;
string m1="";
string com="";
if (requested==settingsHandle)
{
if (data != EOF) {
p=llSubStringIndex(data,"//");
if (p==-1)
{
//データー行
p=llSubStringIndex(data,":");
m1=llGetSubString(data,p+1,llStringLength(data)-1);
com=llGetSubString(data,0,p-1);
if (com=="Partitions") maxNumOfPartitions=(integer)m1;
if (com=="Ra") a=(float)m1;
if (com=="Rb") b=(float)m1;
if (com=="AngleZ") ThetaZ=(float)m1;
if (com=="PositionX") offsetX=(float)m1;
if (com=="PositionY") offsetY=(float)m1;
if (com=="PositionZ") offsetZ=(float)m1;
if (com=="deltaXZ") dXZ=(float)m1;
if (com=="deltaYZ") dYZ=(float)m1;
}
settingsLine++;
settingsHandle=llGetNotecardLine("settings",settingsLine);
}
else
{
//dθ
dTheta=PI/2/maxNumOfPartitions;
//初期位置
x1=a;
isReading=FALSE;
}
}
}
}
設定ファイル(ノートカード:settings)
//90度を何分割するか(正の整数)
Partitions:2
//楕円のX軸方向の半径(正の実数・メートル)
Ra:0.25
//楕円のY軸方向の半径(正の実数・メートル)
Rb:0.2
//ひらひらの縦方向すぼまりの傾き(正の実数・度)。
//プラス指定で上がすぼまるテーパー状に配置されます。
AngleZ:20
//スカートを出現させる装置中心位置からのX位置調整(実数・メートル)
//0でマネキンの位置。
PositionX:0
//スカートを出現させる装置中心位置からのY位置調整(実数・メートル)
//0でマネキンの位置。
PositionY:0
//スカートを出現させる装置中心位置からの高さ調整(実数・メートル)
//値を大きくすると下に下がります。
//パーツのZ軸サイズの半分で大体マネキンの腰のあたりになります。
PositionZ:0.25
//X軸とスカート上端面の傾き(実数・度)
//指定が0以外の場合、前方向から見て傾斜して見えます。
deltaXZ:0
//Y軸とスカート上端面の傾き(実数・度)
//指定が0以外の場合、横方向から見て傾斜して見えます。
deltaYZ:10
2009年08月02日
物体の回転その2(対空砲)
 llRotBetween()という素敵な関数を見つけたのと、箱が傾いて見えるのが気に入らなかったので傾かない箱を。。。
llRotBetween()という素敵な関数を見つけたのと、箱が傾いて見えるのが気に入らなかったので傾かない箱を。。。XY平面上でのX軸(単位ベクトル<1,0,0>)からの回転(水平回転)
rotation newRot=llRotBetween(<1,0,0>,<norm.x,norm.y,0>);
垂直回転
rotation newRot2=llEuler2Rot(<0,llAcos(norm.z)-PI/2.0,0>);
回転実行(順番が大事)
llSetRot(newRot2*newRot);
だいぶシンプルになりました。が、相変わらず思考はvector。。。^^;
ホントにいいのかな、これで。。(笑
対空砲の動きをする箱の中身
default
{
state_entry()
{
llSensorRepeat("","",AGENT|ACTIVE,30,PI,0.1);
}
sensor(integer detectedNum)
{
if (llDetectedKey(0)==llGetOwner() && llDetectedKey(0)!=NULL_KEY)
{
vector targetVector=llDetectedPos(0)-llGetPos();
vector norm=llVecNorm(targetVector);
rotation newRot=llRotBetween(<1,0,0>,<norm.x,norm.y,0>);
rotation newRot2=llEuler2Rot(<0,llAcos(norm.z)-PI/2.0,0>);
llSetRot(newRot2*newRot);
}
}
no_sensor()
{
}
}
2009年07月31日
直交座標系で物体の回転
 エヴァンゲリオンのATフィールドを練習用に作っていて、直交座標上の位置関係から物体を相手の方向に向けてやる必要があったのですが、どうも探しても関数が見つからなかったので。。
エヴァンゲリオンのATフィールドを練習用に作っていて、直交座標上の位置関係から物体を相手の方向に向けてやる必要があったのですが、どうも探しても関数が見つからなかったので。。もっとよい方法があるのかもしれませんが、とりあえず直感的なやり方ということで、直交座標系をRπ座標系に変換してから回転。。
任意の2つのベクトルA,B間の角度は、
cos(θ)=A*B/|A||B|
ここでA*BはAとBの内積。(lslでもそのまま
なので、任意の直交座標系
θx=acos(A.x / |A|)
θy=acos(A.y / |A|)
θz=acos(A.z / |A|)
llGetNorm(A)で先にAの方向を向いている単位ベクトルA'を求めておけば、
θx=acos(A'.x)
θy=acos(A'.y)
θz=acos(A'.z)
手順としては自分と対象の位置を求め、この2ベクトルの差を求め、その単位ベクトルを求め、座標系をRπに変えて、向きを変えてやる、という順の処理。(処理というほどでもないですか。。)
三角関数は0~180度の範囲しか値を取れないので、y軸の値の正負によって180~360度の間を場合分けして補正。これで本当にいいのでしょうか。。^^;
まぁ、動いているからいいんだけど。。^^;;;
8・2追記
短くしてもう少しきれいに回るようにしました。
http://rbk.slmame.com/e696560.html
半径5メートルに近づいた物体の方向にx面を向ける箱の中身。
default
{
state_entry()
{
llSensorRepeat("","",AGENT|ACTIVE,5,PI,0.1);
}
sensor(integer detectedNum)
{
if (llDetectedKey(0)!=NULL_KEY)
{
//自分原点で、ターゲットのベクトル
vector targetVector=llDetectedPos(0)-llGetPos();
//その単位ベクトル
vector norm=llVecNorm(targetVector);
//座標系をRπに変換
float thita_x=llAcos(norm*<1,0,0>);
float thita_y=llAcos(norm*<0,1,0>);
float thita_z=llAcos(norm*<0,0,1>);
//値が180度を超えた場合(Y値がマイナス)
if (norm.y<0) {
thita_x*=-1;
thita_z=PI-thita_z;
}
//回転実行
llSetRot(llAxisAngle2Rot(<0,0,1>,thita_x)*llAxisAngle2Rot(<1,0,0>,(thita_z-PI/2)*-1));
}
}
no_sensor()
{
}
}




